题目内容
3.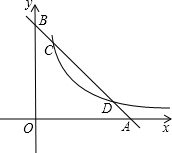 已知:一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}(x>0)$的图象交于点C、D,且$\frac{BD}{BA}=\frac{2}{3}$.
已知:一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}(x>0)$的图象交于点C、D,且$\frac{BD}{BA}=\frac{2}{3}$.(1)求∠BAO的度数;
(2)求O到BC的距离.
分析 (1)在y=-x+b中,令y=0,则x=b,令x=0,y=b,求得OA=b,OB=b,得到tan∠BAO=$\frac{OB}{OA}$=1,即可得到结论;
(2)过D作DE⊥x轴于E,根据相似三角形的性质得到$\frac{AE}{OA}=\frac{DE}{OB}=\frac{AD}{AB}$,点D在一次函数y=-x+b的图象上,设D(m,-m+b),由已知条件得到$\frac{AD}{AB}=\frac{1}{3}$,得到$\frac{b-m}{b}=\frac{1}{3}$,①,由点D反比例函数$y=\frac{5}{x}(x>0)$的图象上,得到m(-m+b)=5,②,①,②联立方程组解得得到得到OA=OB=$\frac{3\sqrt{10}}{2}$,根据等腰直角三角形的性质得到结论.
解答 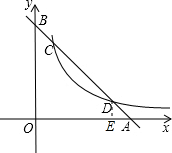 解:(1)在y=-x+b中,令y=0,则x=b,令x=0,y=b,
解:(1)在y=-x+b中,令y=0,则x=b,令x=0,y=b,
∴A(b,0),B(0,b),
∴OA=b,OB=b,
∴tan∠BAO=$\frac{OB}{OA}$=1,
∴∠BAO=45°;
(2)过D作DE⊥x轴于E,
∴DE∥OB,
∴△ADE∽△AOB,
∴$\frac{AE}{OA}=\frac{DE}{OB}=\frac{AD}{AB}$,
∵点D在一次函数y=-x+b的图象上,
∴设D(m,-m+b),
∵$\frac{BD}{BA}=\frac{2}{3}$,
∴$\frac{AD}{AB}=\frac{1}{3}$,
∴$\frac{b-m}{b}=\frac{1}{3}$,①,
∵点D反比例函数$y=\frac{5}{x}(x>0)$的图象上,
∴m(-m+b)=5,②,
①,②联立方程组解得m=±$\sqrt{10}$,
∵D在第一象限,
∴m=$\sqrt{10}$,
∴b=$\frac{3\sqrt{10}}{2}$,
∴OA=OB=$\frac{3\sqrt{10}}{2}$,
∴AB=$\sqrt{2}$OA=3$\sqrt{5}$,
∴O到BC的距离=$\frac{1}{2}$AB=$\frac{3\sqrt{5}}{2}$.
点评 本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.

 购买一种水果,所付款金额(元)与购买数量(千克)之间的函数图象由线段OA和射线AB组成,如图所示,则一次购买20千克这种水果,比分两次每次购买10千克这种水果可以节省的费用为( )
购买一种水果,所付款金额(元)与购买数量(千克)之间的函数图象由线段OA和射线AB组成,如图所示,则一次购买20千克这种水果,比分两次每次购买10千克这种水果可以节省的费用为( )| A. | 20元 | B. | 12元 | C. | 10元 | D. | 8元 |
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
| A. | 1:2:2:1 | B. | 2:1:1:1 | C. | 1:2:3:4 | D. | 2:1:2:1 |
 如图,平行四边形中,AE⊥BC于E,AF⊥CD于F.
如图,平行四边形中,AE⊥BC于E,AF⊥CD于F.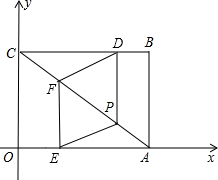 在直角坐标系中,点O为原点,点B的坐标为(4,3),四边形ABCO是矩形,点D从B出发以每秒1个单位的速度向终点C运动,同时点E从O点出发以每秒1个单位的速度向终点A运动,过D作DP⊥BC与AC交于点P,过E作EF⊥AO与AC交于点F,连结DF、PE.
在直角坐标系中,点O为原点,点B的坐标为(4,3),四边形ABCO是矩形,点D从B出发以每秒1个单位的速度向终点C运动,同时点E从O点出发以每秒1个单位的速度向终点A运动,过D作DP⊥BC与AC交于点P,过E作EF⊥AO与AC交于点F,连结DF、PE. 已知△ABC的顶点A、B、C的坐标分别是(-3,0)、(-1,2)、(-2,4).
已知△ABC的顶点A、B、C的坐标分别是(-3,0)、(-1,2)、(-2,4).