题目内容
18.完成下列计算和解方程题(1)|$\sqrt{6}$-$\sqrt{2}$|+|$\sqrt{2}$-1|-|3-$\sqrt{6}$|
(2)$\root{3}{\frac{27}{8}}$-$\root{3}{1-\frac{189}{64}}$-$\sqrt{1-\frac{31}{256}}$
(3)(x-1)2-81=0
(4)8(x+2)3+27=0.
分析 (1)先计算绝对值,再合并同类项即可求解;
(2)先计算立方根和算术平方根,再计算减法即可求解;
(3)先变形为(x-1)2=81,再根据平方根的定义计算即可求解;
(4)先变形为(x+2)3=-$\frac{27}{8}$,再根据立方根的定义计算即可求解.
解答 解:(1)|$\sqrt{6}$-$\sqrt{2}$|+|$\sqrt{2}$-1|-|3-$\sqrt{6}$|
=$\sqrt{6}$-$\sqrt{2}$+$\sqrt{2}$-1-3+$\sqrt{6}$
=2$\sqrt{6}$-4;
(2)$\root{3}{\frac{27}{8}}$-$\root{3}{1-\frac{189}{64}}$-$\sqrt{1-\frac{31}{256}}$
=$\frac{3}{2}$+$\frac{5}{4}$-$\frac{15}{16}$
=$\frac{29}{16}$;
(3)(x-1)2-81=0,
(x-1)2=81,
x-1=±9,
x=-8或x=10;
(4)8(x+2)3+27=0,
8(x+2)3=-27,
(x+2)3=-$\frac{27}{8}$,
x+2=-$\frac{3}{2}$,
x=-$\frac{7}{2}$.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握立方根、算术平方根、平方根和绝对值等考点的运算.

练习册系列答案
相关题目
9.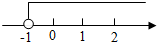 已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )
已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )
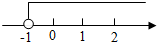 已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )
已知关于x的不等式2x-a>-3的解集在数轴上表示如图所示,则a的值等于( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
13.在数轴上到原点的距离等于5的点表示的数是( )
| A. | 5 | B. | 2 | C. | 5或-2 | D. | 5或-5 |
3.下列各式的计算中,结果为2$\sqrt{5}$的是( )
| A. | $\sqrt{2}×\sqrt{10}$ | B. | $\sqrt{8}×\sqrt{5}$ | C. | $\sqrt{10}÷\sqrt{2}$ | D. | $\sqrt{\frac{1}{2}}÷\sqrt{\frac{1}{80}}$ |
7.下列计算正确的是( )
| A. | (-1)-3=1 | B. | (-4)0=1 | C. | (-2)2×(-2)-3=26 | D. | 2a-4=$\frac{1}{{2a}^{4}}$ |