题目内容
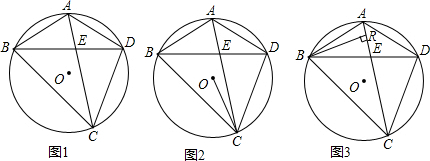
8.已知:如图1,四边形ABCD内接于⊙O,AC、BD交于点E,AB=AD.(1)求证:AC平分∠BCD;
(2)如图2,连接CO,若∠CAD=2∠OCB,求证:BD=BC;
(3)在(2)的条件下,如图3,BR⊥AC交AC于点R,tan∠ACD=$\frac{\sqrt{7}}{3}$,AR=1,求CD长.
分析 (1)根据圆的性质即可得到结论;
(2)如图2,连接DO,延长CO交BD于F,设∠BCO=x°,则∠DBC=∠CAD=2∠BCO=2x°,由已知条件得到∠DOC=2∠DBC=4x°,∠DFC=∠DBC+∠BCF=3x°,根据角的和差得到∠BDO=∠DOC-∠DFC=4x-3x=x°,等量代换得到∠BCD=∠BDC,根据等腰三角形的判定定理即可得到结论;
(3)作BF⊥AD于F,推出△FBA≌△RBA,根据全等三角形的性质得到FA=RA=1,解直角三角形得到tan∠ACB═$\frac{\sqrt{7}}{3}$,设BF=$\sqrt{7}$a,FD=3a,得到AB=AD=3a-1,根据勾股定理列方程得到AB=AD=8,BC=BD=12,延长CD至K,使DK=BC,连接AK,解直角三角形即可得到结论.
解答 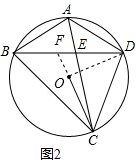 解:(1)∵AB=AD,
解:(1)∵AB=AD,
∴弧AB=弧AD,
∴∠ACB=∠ACD;
(2)如图2,连接DO,延长CO交BD于F,
设∠BCO=x°,则∠DBC=∠CAD=2∠BCO=2x°,
∴∠DOC=2∠DBC=4x°,∠DFC=∠DBC+∠BCF=3x°,
∴∠BDO=∠DOC-∠DFC=4x-3x=x°,
∴∠BCO=∠BDO,
∵DO=CO,
∴∠OCD=∠ODC,
∠BCO+∠OCD=∠BDO+∠ODC,
∴∠BCD=∠BDC,
∴BD=CD;
(3)如图3,作BF⊥AD于F,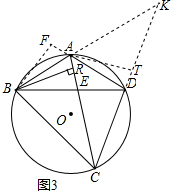
∵∠BDC=∠BCD,∠BDC=∠BAC,
∴∠BCD=∠BAC,
∵∠BCD+∠BAD=∠BAD+∠BAF=180°,
∴∠BCD=∠BAF,
在△FBA与△RBA中,
$\left\{\begin{array}{l}{∠BCD=∠BAF}\\{∠BFA=∠BRA}\\{AB=AB}\end{array}\right.$,
∴△FBA≌△RBA,
∴FA=RA=1,
∵∠BDA=∠BCA,tan∠ACB=$\frac{\sqrt{7}}{3}$,
∴tan∠ACB═$\frac{\sqrt{7}}{3}$,
∴设BF=$\sqrt{7}$a,FD=3a,
∴AB=AD=3a-1,
∴AB2=AF2+BF2,a=3,AB=AD=8,BC=BD=12,
延长CD至K,使DK=BC,连接AK,
则△ABC≌△ADK,AC=10,
作AT⊥CK,
∵AC=AK,
∴CK=2CT,
CT=AC•cos∠ACD=7.5,
∴CD=CK-DK=15-12=3.
点评 本题考查了圆的性质,全等三角形的判定和性质,解直角三角形,勾股定理,等腰三角形的判定和性质,作辅助线构造全等三角形是解题的关键.

| A. | 43×108 | B. | 4.3×109 | C. | 4.3×108 | D. | 4.3×1010 |
| A. | ${(-\sqrt{3})^2}=-3$ | B. | $\sqrt{{{(π-3.2)}^2}}=π-3.2$ | C. | ${(2\sqrt{6})^2}=24$ | D. | $\sqrt{{{(-3)}^2}}=-3$ |
| A. | -32 | B. | |-3| | C. | (-3)2 | D. | -(-3) |
| A. | 345 | B. | 357 | C. | 456 | D. | 567 |
| A. | 若x>y,则x2>y2 | B. | 若|a|=|b|,则a=b | C. | 若a>|b|,则a2>b2 | D. | 若a<1,则a>$\frac{1}{a}$ |

 如图,木条a与木条c垂直,将木条a绕点O旋转后与木条b平行,则旋转角的最小值为22°.
如图,木条a与木条c垂直,将木条a绕点O旋转后与木条b平行,则旋转角的最小值为22°.