题目内容
9. 计算或证明(证明过程必须批注理由)
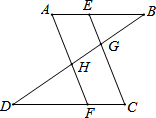
计算或证明(证明过程必须批注理由)(1)如图,已知∠A=∠C,∠DHF=∠EGB.求证:∠D=∠B
(2)3$\sqrt{\frac{1}{3}}$-($\sqrt{3}$-2)2-3$\sqrt{2}$$÷\sqrt{\frac{3}{2}}$+($\sqrt{2}$)-1-$\root{3}{-8}$.
分析 (1)根据对顶角相等,和已知条件得到∠AHB=∠EGB,根据平行线的判定得到AF∥EC,由平行线的性质得到∠C=∠AFD,推出AB∥DC,根据平行线的性质即可得到结论.
(2)根据实数的运算法则计算即可.
解答 (1)证明:∵∠DHF=∠AHB(对顶角相等),
∠DHF=∠EGB(已知),
∴∠AHB=∠EGB(等量代换),
∴AF∥EC(同位角相等,二直线平行),
∴∠C=∠AFD(二直线平行,同位角相等),
又∵∠C=∠A(已知),
∴∠A=∠AFD(等量代换),
∴AB∥DC(内错角相等,二直线平行),
∴∠D=∠B (二直线平行,内错角相等),
(2)3$\sqrt{\frac{1}{3}}$-($\sqrt{3}$-2)2-3$\sqrt{2}$$÷\sqrt{\frac{3}{2}}$+($\sqrt{2}$)-1-$\root{3}{-8}$=$\sqrt{3}$-7+4$\sqrt{3}$-2$\sqrt{3}$+$\frac{\sqrt{2}}{2}$+2=3$\sqrt{3}$-5+$\frac{\sqrt{2}}{2}$.
点评 本题考查了平行线的判定和性质,实数的运算,负整数指数幂,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
20.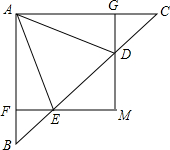 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )| A. | △CAE∽△BDA | B. | $\frac{AD}{AE}=\frac{AC}{BD}$ | C. | BD•CE=4 | D. | BE=$\sqrt{2}$BF |
4.已知四个三角形分别满足下列条件:①三角形的三边之比为1:1:$\sqrt{2}$;②三角形的三边分别是9、40、41;③三角形三内角之比为1:2:3;④三角形一边上的中线等于这边的一半.其中直角三角形有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
14.三角形中,三个内角的比为1:3:6,它的三个外角的比为( )
| A. | 1:3:6 | B. | 6:3:1 | C. | 9:7:4 | D. | 4:7:9 |
1.已知点M(3,-4),那么M到原点的距离是( )
| A. | 3 | B. | 4 | C. | -4 | D. | 5 |
18. 如图,在直线l上有三个正方形A,B,C,若正方形A,C的面积分别是8,6,则正方形B的面积为( )
如图,在直线l上有三个正方形A,B,C,若正方形A,C的面积分别是8,6,则正方形B的面积为( )
 如图,在直线l上有三个正方形A,B,C,若正方形A,C的面积分别是8,6,则正方形B的面积为( )
如图,在直线l上有三个正方形A,B,C,若正方形A,C的面积分别是8,6,则正方形B的面积为( )| A. | 10 | B. | 12 | C. | 14 | D. | 18 |
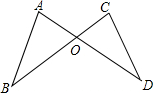 如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.
如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.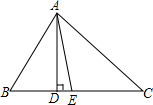 如图,在△ABC中,∠B=63°,∠C=47°,AD和AE分别是它的高和角平分线,则
如图,在△ABC中,∠B=63°,∠C=47°,AD和AE分别是它的高和角平分线,则