题目内容
19.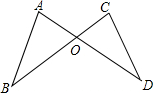 如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.
如图,已知AD与BC相交于点O,AB=CD,AD=BC,求证∠A=∠C;请把题中的结论∠A=∠C和已知条件AB=CD,AD=BC中的一个作为条件,另一个作为结论,形成真命题,并加以证明.
分析 连接BD,由SSS证明△ABD≌△CDB,即可得出∠A=∠C;由AAS证明△AOB≌△COD,得出对应边相等OA=OC,OB=OD,即可得出AD=BC.
解答 证明:连接BD,如图所示:
在△ABD和△CDB中,
$\left\{\begin{array}{l}{AB=CD}&{\;}\\{AD=CB}&{\;}\\{BD=DB}&{\;}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
∴∠A=∠C;
真命题:已知:∠A=∠C,AB=CD,
求证:AD=BC,
证明:在△AOB和△COD中,
$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{∠AOB=∠COD}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△AOB≌△COD(AAS),
∴OA=OC,OB=OD,
∴OA+OD=OC+OB,
即AD=BC.
点评 本题考查了全等三角形的判定与性质;熟记三角形全等的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
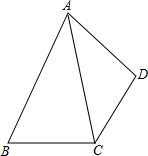 如图,AC平分∠BAD,CD=CB,AB>AD,求证:∠B+∠ADC=180°.
如图,AC平分∠BAD,CD=CB,AB>AD,求证:∠B+∠ADC=180°. 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( ) 如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO. 如图,点A在数轴上表示的数是-4,点B表示的数是+8,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴运动,设运动时间为t(秒).
如图,点A在数轴上表示的数是-4,点B表示的数是+8,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴运动,设运动时间为t(秒). 计算或证明(证明过程必须批注理由)
计算或证明(证明过程必须批注理由)