题目内容
18. 如图,在直线l上有三个正方形A,B,C,若正方形A,C的面积分别是8,6,则正方形B的面积为( )
如图,在直线l上有三个正方形A,B,C,若正方形A,C的面积分别是8,6,则正方形B的面积为( )| A. | 10 | B. | 12 | C. | 14 | D. | 18 |
分析 运用正方形边长相等,再根据同角的余角相等可得∠EDF=∠HFG,然后证明△EDF≌△HFG,再结合全等三角形的性质和勾股定理来求解即可.
解答 解:如图,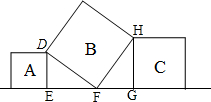
由于A、B、C都是正方形,所以DF=FH,∠DFH=90°;
∵∠DFE+∠HFG=∠EDF+∠DFE=90°,即∠EDF=∠HFG,
在△DEF和△HGF中,
$\left\{\begin{array}{l}{∠EDF=∠HFG}\\{∠DEF=∠HGF}\\{DF=HF}\end{array}\right.$,
∴△ACB≌△DCE(AAS),
∴DE=FG,EF=HG;
在Rt△ABC中,由勾股定理得:DF2=DE2+EF2=DE2+HG2,
即SB=SA+SC=8+6=14,
故选:C.
点评 此题主要考查全等三角形的判定和性质,和勾股定理,关键是证明△DEF≌△HGF.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
10.利用墙的一边和长为39米的铁丝网,围成一个面积为180平方米的矩形,设这个矩形垂直于墙的一边长为x米,则根据题意可以列出正确的方程是( )
| A. | 2x2-39x+180=0 | B. | 2x2+39x+180=0 | C. | 2x2-39x-180=0 | D. | 2x2+39x-180=0 |
7.一组数据为6,12,12,15,9,27,12,15,3,24,其众数、中位数及平均数分别是( )
| A. | 12,12,18 | B. | 12,12,13.5 | C. | 12,18,13.5 | D. | 15,18,13.5 |
 如图,点A在数轴上表示的数是-4,点B表示的数是+8,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴运动,设运动时间为t(秒).
如图,点A在数轴上表示的数是-4,点B表示的数是+8,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴运动,设运动时间为t(秒).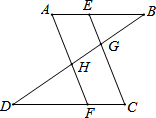 计算或证明(证明过程必须批注理由)
计算或证明(证明过程必须批注理由)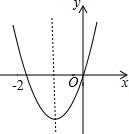 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2a;④am2+bm+a>0(m≠-1);⑤设A(100,y1),B(-100,y2)在该抛物线上,则y1>y2.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①c=0;②该抛物线的对称轴是直线x=-1;③当x=1时,y=2a;④am2+bm+a>0(m≠-1);⑤设A(100,y1),B(-100,y2)在该抛物线上,则y1>y2.