题目内容

17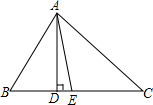．如图，在△ABC中，∠B=63°，∠C=47°，AD和AE分别是它的高和角平分线，则
∠DAE=8°．

分析 根据三角形的内角和等于180°求出∠BAC，再根据角平分线的定义求出∠BAE，根据直角三角形两锐角互余求出∠BAD，然后根据∠DAE=∠BAE-∠BAD计算即可得解．

解答 解：∵∠B=63°，∠C=47°，
∴∠BAC=180°-∠B-∠C=180°-63°-47°=70°，
∵AE是三角形的平分线，
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×70°=35°，
∵AD是三角形的高，
∴∠BAD=90°-∠B=90°-63°=27°，
∴∠DAE=∠BAE-∠BAD=35°-27°=8°．
故答案为：8．

点评 本题考查了三角形的内角和定理，三角形的角平分线的定义，高线的定义，是基础题，熟记定理与概念并准确识图，理清图中各角度之间的关系是解题的关键．

练习册系列答案
相关题目
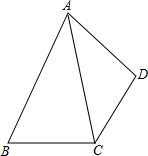7．如图，AC平分∠BAD，CD=CB，AB＞AD，求证：∠B+∠ADC=180°．
8．如图，点A在数轴上表示的数是-4，点B表示的数是+8，P，Q两点同时分别以1个单位/秒和2个单位/秒的速度从A，B两点出发，沿数轴运动，设运动时间为t（秒）．
（1）线段AB的长度为12个单位；
（2）如果点P向右运动，点Q向左运动，几秒后PQ=$\frac{1}{2}$AB？
（3）如果点P，Q同时向左运动，M，N分别是PA和BQ的中点，是否存在这样的时间t使得线段MN=$\frac{1}{4}$AB？若存在，求出t的值；若不存在，请说明理由．
5．观察下面一组式子：
（1）1×$\frac{1}{2}=1-\frac{1}{2}$；（2）$\frac{1}{2}×\frac{1}{3}=\frac{1}{2}-\frac{1}{3}$；
（3）$\frac{1}{3}×\frac{1}{4}=\frac{1}{3}-\frac{1}{4}$；（4）$\frac{1}{4}×\frac{1}{5}=\frac{1}{4}-\frac{1}{5}$…
写出这组式子中的第（n）组式子是$\frac{1}{n}×\frac{1}{n+1}=\frac{1}{n}-\frac{1}{n+1}$．
12．如果3a-2b=2，那么9a-6b的值是6．
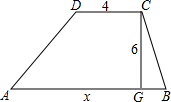2．如图，梯形ABCD上底的长是4，下底的长是x，高是6．
（1）求梯形ABCD的面积y与下底长x之间的关系式；
（2）用表格表示当x从10变到16时（每次增加1），y的相应值；
（3）x每增加1时，y如何变化？说明你的理由．
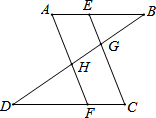9．计算或证明（证明过程必须批注理由）
（1）如图，已知∠A=∠C，∠DHF=∠EGB．求证：∠D=∠B
（2）3$\sqrt{\frac{1}{3}}$-（$\sqrt{3}$-2）2-3$\sqrt{2}$$÷\sqrt{\frac{3}{2}}$+（$\sqrt{2}$）-1-$\root{3}{-8}$．
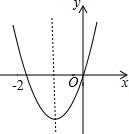6．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①c=0；②该抛物线的对称轴是直线x=-1；③当x=1时，y=2a；④am2+bm+a＞0（m≠-1）；⑤设A（100，y1），B（-100，y2）在该抛物线上，则y1＞y2．
其中正确的结论有①②④⑤．（写出所有正确结论的序号）
7．一组数据为6，12，12，15，9，27，12，15，3，24，其众数、中位数及平均数分别是（　　）
A．12，12，18B．12，12，13.5C．12，18，13.5D．15，18，13.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网