题目内容
4.已知四个三角形分别满足下列条件:①三角形的三边之比为1:1:$\sqrt{2}$;②三角形的三边分别是9、40、41;③三角形三内角之比为1:2:3;④三角形一边上的中线等于这边的一半.其中直角三角形有( )个.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据勾股定理的逆定理或三角形的内角和定理即可进行判断,从而得到答案.
解答 解:①因为12+12=($\sqrt{2}$)2三边符合勾股定理的逆定理,故是直角三角形;
②因为92+402=412三边符合勾股定理的逆定理,故是直角三角形;
③设最小的角为x,则x+2x+3x=180°,则三角分别为30°,60°,90°,故是直角三角形;
④因为符合直角三角形的判定,故是直角三角形.
所以有4个直角三角形.
故选:A.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
14. 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
 如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )
如图,△ABC,△ADE均为等边三角形,AD平分∠BAC交BC于点D,DE交AB于点F.下列结论:①AD⊥BC;②EF=DF;③BE=BD;④BE∥AC.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.下列调查中,适用普查方法的是( )
| A. | 了解一批袋装食品是否含有防腐剂 | |
| B. | 了解某班学生“50米跑”的成绩 | |
| C. | 了解江苏卫士“非诚勿扰”节目的收视率 | |
| D. | 调查我市冷饮市场雪糕质量情况 |
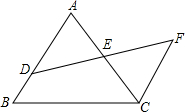 如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
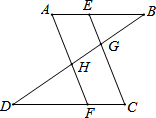 计算或证明(证明过程必须批注理由)
计算或证明(证明过程必须批注理由)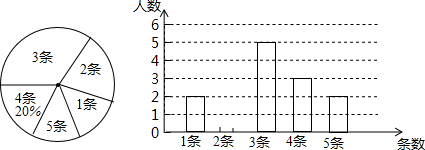
 某球队14名队员的年龄统计如图所示,则球队队员的年龄的众数、中位数分别是17、16.
某球队14名队员的年龄统计如图所示,则球队队员的年龄的众数、中位数分别是17、16.