题目内容
20.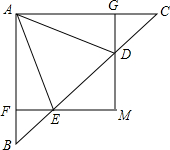 如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )
如图,在△ABC中,∠BAC=90°,D,E为BC上两点,过点D,E分别作AC,AB的垂线,两垂线交于点M,垂足分别为G,F,若∠AED=∠BAD,AB=AC=2,则下列说法中不正确的是( )| A. | △CAE∽△BDA | B. | $\frac{AD}{AE}=\frac{AC}{BD}$ | C. | BD•CE=4 | D. | BE=$\sqrt{2}$BF |
分析 根据等腰直角三角形的性质得到∠B=∠C=45°,推出△CAE∽△BDA,由相似三角形的性质得到$\frac{AC}{BD}=\frac{CE}{AB}=\frac{AD}{AE}$,证得BD•CE=4,由EF⊥AB,得到△BEF是等腰直角三角形,于是得到BE=$\sqrt{2}$BF,即可得到结论.
解答  解:∵∠BAC=90°,AB=AC,
解:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵∠AED=∠BAD,
∴△CAE∽△BDA,
∴AC:BD=CE:AB=AE:AD,
∵AB=AC=2,
∴BD•CE=4,
∵EF⊥AB,
∴△BEF是等腰直角三角形,
∴BE=$\sqrt{2}$BF,
∴A、C、D正确,
故选B.
点评 本题考查了相似三角形的判定和性质,正方形的性质,等腰直角三角形的性质,正确的识图是解题的关键.

练习册系列答案
相关题目
10.利用墙的一边和长为39米的铁丝网,围成一个面积为180平方米的矩形,设这个矩形垂直于墙的一边长为x米,则根据题意可以列出正确的方程是( )
| A. | 2x2-39x+180=0 | B. | 2x2+39x+180=0 | C. | 2x2-39x-180=0 | D. | 2x2+39x-180=0 |
 如图,点A在数轴上表示的数是-4,点B表示的数是+8,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴运动,设运动时间为t(秒).
如图,点A在数轴上表示的数是-4,点B表示的数是+8,P,Q两点同时分别以1个单位/秒和2个单位/秒的速度从A,B两点出发,沿数轴运动,设运动时间为t(秒).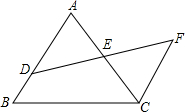 如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.
如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=5.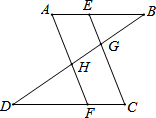 计算或证明(证明过程必须批注理由)
计算或证明(证明过程必须批注理由)