题目内容
20．
如图所示，数轴上表示1，$\sqrt{2}$的对应点分别为A，B，沿过点A的直线折叠，点B落在数轴上的点C处，设点C所表示的数为x，求$\frac{{x}^{2}+2}{x}$的值．
分析 根据中点坐标公式，可得x的值，根据代数式求值，可得答案．
解答 解：由题意，得
$\frac{x+\sqrt{2}}{2}$=1，
解得x=2-$\sqrt{2}$．
$\frac{{x}^{2}+2}{x}$=$\frac{（2-\sqrt{2}）^{2}+2}{2-\sqrt{2}}$=4．
点评 本题考查了实数与数轴，利用中点坐标公式得出x的值是解题关键．
练习册系列答案
相关题目
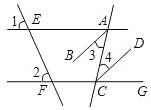如图，直线AE、CF分别被直线EF、AC所截，已知，∠1=∠2，AB平分∠EAC，CD平分∠ACG．将下列证明AB∥CD的过程及理由填写完整．
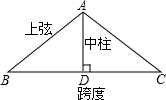如图，厂房屋顶人字架（等腰三角形）的跨度为20m，∠B=37°，求中柱AD（D为底边中点）和上弦AB的长（参考数据：cos37°≈0.6）
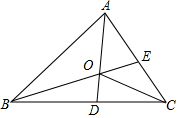如图，AD和BE是△ABC的角平分线且交于点O，连接OC，现有以下论断：