题目内容
5．
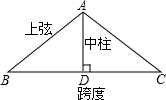如图，厂房屋顶人字架（等腰三角形）的跨度为20m，∠B=37°，求中柱AD（D为底边中点）和上弦AB的长（参考数据：cos37°≈0.6）
分析 直接利用等腰三角形的性质得出BD=DC，再利用锐角三角函数关系结合勾股定理得出答案．
解答 解：如图所示：∵AB=AC，BC=20m，AD⊥BC，
∴BD=DC=10m，
∴cos37°=$\frac{BD}{AB}$=0.6，
则AB=$\frac{10}{\frac{3}{5}}$=$\frac{50}{3}$（m），
故AD=$\sqrt{（\frac{50}{3}）^{2}-1{0}^{2}}$=$\frac{40}{3}$（m），
答：中柱AD（D为底边中点）为$\frac{40}{3}$m和上弦AB的长为$\frac{50}{3}$m．
点评 此题主要考查了解直角三角形的应用和勾股定理，正确得出BD的长是解题关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
15．
如图是一个五角星图案，则∠A+∠B+∠C+∠D+∠E的度数是（ ）
如图是一个五角星图案，则∠A+∠B+∠C+∠D+∠E的度数是（ ）| A． | 180° | B． | 150° | C． | 135° | D． | 120° |
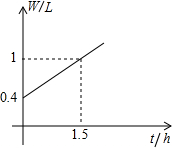水龙头关闭不严就会滴水，现在没拧紧的水龙头下面放一个容器，容器内的盛水量W（L）与滴水时间t（h）的关系如图所示，给合图象解答下列问题：
如图所示，数轴上表示1，$\sqrt{2}$的对应点分别为A，B，沿过点A的直线折叠，点B落在数轴上的点C处，设点C所表示的数为x，求$\frac{{x}^{2}+2}{x}$的值．
如图，平行四边形ABCD中，∠ABC=75°，AF⊥BC，垂足为F，AF交BD于E，若DE=2AB，求∠AED的度数．
如图，四边形ABCD是正方形，以B点为圆心，BD的长为半径画弧交BC延长线于点E，以DE为边作正方形DEFG，作FH⊥BE交BE的延长线于点H，连接AE、CG，则下列结论中正确的有（ ）
如图，AB是⊙O的一条弦，C，D是⊙O上的两个动点，且在AB弦的异侧，连接CD．