题目内容
7.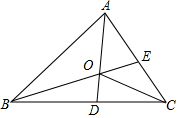 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:①OD⊥BC;
②∠AOC=90°+$\frac{1}{2}$∠ABC;
③OA=OB=OC;
④OC平分∠ACB;
⑤∠AOE+∠DCO=90°
其中正确的有②④⑤.
分析 根据角平分线的性质可对①进行判断;利用三角形的角平分线相交于一点可对④进行判断;根据三角形内心的性质可对③进行判断;根据角平分线的定义和三角形的内角和可对②⑤进行判断.
解答 解:∵AD是△ABC的角平分线,
∴AD不一定垂直BC,所以①错误;
∵AD和BE是△ABC的角平分线,
∴CO平分∠BOC,所以④正确;
∴∠AOC=180°-∠OAC-∠OCA=180°-$\frac{1}{2}$∠BAC-$\frac{1}{2}$∠BCA=180°-$\frac{1}{2}$(180°-∠ABC)=90°+$\frac{1}{2}$∠ABC,所以②正确;
∵点O为△ABC的内心,
∴OB、OC、OD不一定都相等,所以③错误;
∵∠AOE=∠OBA+∠OAB,
∴∠AOE+∠DCO=∠OBA+∠OAB+∠DCO=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$×180°=90°,所以⑤正确.
故答案为②④⑤.
点评 本题考查了三角形内角和定理:三角形内角是三角形三边的夹角.每个三角形都有三个内角,且每个内角均大于0°且小于180°.记住三角形内角和是180°

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
2.手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如表:则这两个模型都制作完成所需的最短时间为22分钟.
| 工序 时间 模型 | 打磨(A组) | 组装(B组) |
| 模型甲 | 9分钟 | 5分钟 |
| 模型乙 | 6分钟 | 11分钟 |
 如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.
如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.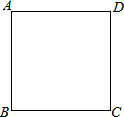 如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?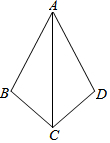 如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC.那么可添加条件为∠BAC=∠DAC.
如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC.那么可添加条件为∠BAC=∠DAC.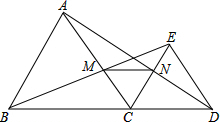 如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.