题目内容
15.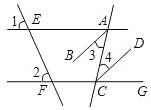 如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.证明:∵∠1=∠2,
∴AE∥CF,(同位角相等,两直线平行)
∴∠EAC=∠ACG,(两直线平行,内错角相等)
∵AB平分∠EAC,CD平分∠ACG,
∴2∠3=∠EAC,2∠4=∠ACG,
∴∠3=∠4,
∴AB∥CD(内错角相等,两直线平行).
分析 首先证明AE∥CF,进而得到∠EAC=∠ACG,再利用角平分线的性质得到∠3=∠4,于是得到AB∥CD.
解答 证明:∵∠1=∠2,
∴AE∥CF,(同位角相等,两直线平行)
∴∠EAC=∠ACG,(两直线平行,内错角相等)
∵AB平分∠EAC,CD平分∠ACG,
∴2∠3=∠EAC,2∠4=∠ACG,
∴∠3=∠4,
∴AB∥CD(内错角相等,两直线平行).
故答案为AE;CF;同位角相等,两直线平行;两直线平行,内错角相等;2∠3;2∠4;∠3;∠4;内错角相等,两直线平行
点评 本题考查了平行线的判定和性质、角平分线的定义,解题的关键是理清角之间的关系.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
5. 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )| A. | -10 | B. | 10 | C. | -8 | D. | 8 |
1.甲、乙两地火车线路比汽车线路长30千米,汽车从甲地先开出,速度为40千米/时,开出半小时后,火车也从甲地开出,速度为60千米/时,结果汽车仅比火车晚1小时到达乙地,求甲、乙两地的火车与汽车线路长.
2.手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如表:则这两个模型都制作完成所需的最短时间为22分钟.
| 工序 时间 模型 | 打磨(A组) | 组装(B组) |
| 模型甲 | 9分钟 | 5分钟 |
| 模型乙 | 6分钟 | 11分钟 |
 如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B
如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B 如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.
如图所示,数轴上表示1,$\sqrt{2}$的对应点分别为A,B,沿过点A的直线折叠,点B落在数轴上的点C处,设点C所表示的数为x,求$\frac{{x}^{2}+2}{x}$的值.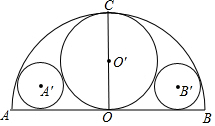 已知:如图,以AB为直径作半圆,半径OC⊥AB,以OC为直径作⊙OO′,再作⊙A′和⊙B都与AB、⊙O及⊙O′相切,如果AB=2R,求⊙A′的半径.
已知:如图,以AB为直径作半圆,半径OC⊥AB,以OC为直径作⊙OO′,再作⊙A′和⊙B都与AB、⊙O及⊙O′相切,如果AB=2R,求⊙A′的半径.