题目内容
17.对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )| A. | m≥-2 | B. | -4≤m≤-2 | C. | m≥-4 | D. | m≤-4或m≥-2 |
分析 分三种情况进行讨论:对称轴分别为x<0、0≤x<2、x≥2时,得出当0<x≤2时所对应的函数值,判断正误.
解答 解:对称轴为:x=-$\frac{b}{2a}$=-$\frac{m}{2}$,y=$\frac{4ac-{b}^{2}}{4a}$=1-$\frac{{m}^{2}}{4}$,
分三种情况:①当对称轴x<0时,即-$\frac{m}{2}$<0,m>0,满足当0<x≤2时的函数值总是非负数;
②当0≤x<2时,0≤-$\frac{m}{2}$<2,-4<m≤0,当1-$\frac{{m}^{2}}{4}$>0时,-2<m≤2,满足当0<x≤2时的函数值总是非负数;
当1-$\frac{{m}^{2}}{4}$<0时,不能满足当0<x≤2时的函数值总是非负数;
∴当-2<m≤0时,当0<x≤2时的函数值总是非负数,
③当对称轴-$\frac{m}{2}$≥2时,即m≤-4,如果满足当0<x≤2时的函数值总是非负数,则有x=2时,y≥0,
4+2m+1≥0,
m≥-$\frac{5}{2}$,
此种情况m无解;
故选A.
点评 本题考查了二次函数的图象及性质,根据其自变量的取值确定字母系数的取值范围,解决此类问题:首先要计算出顶点坐标,再根据对称轴的位置并与图象相结合得出取值.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
5. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
9.某电器超市销售每台进价分别200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第一周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?
6.如图,某数学小组在课外实践活动中,用电钻将四个质地均匀、质量相等的木质小正方体,分别从不同方向钻一个直径一样的直圆孔,再用天平分别称得下列小正方体的质量,下列说法中正确的是( )
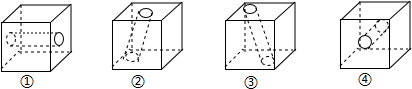

| A. | ①和④更重 | B. | ③最轻 | C. | 质量仍然一样 | D. | ②和③更重 |
 如图,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,已知∠A=30°,∠1=20°,求∠2的度数.
如图,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点A′的位置,已知∠A=30°,∠1=20°,求∠2的度数.