题目内容
10．
如图，已知△ABC和△A′B′C′关于直线MN对称，点P是直线MN上一点，连接PA、PA′、AA′，下列结论错误的是（ ）| A． | ∠B=∠B′ | B． | PA=PA′ | ||
| C． | BC=AA′ | D． | MN是线段AA′的垂直平分线 |
分析 根据△ABC和△A′B′C′关于直线MN对称，即可得到△ABC和△A′B′C′全等，MN是线段AA′的垂直平分线，再根据点P是直线MN上一点，即可得出PA=PA′，据此可得结论．
解答 解：∵△ABC和△A′B′C′关于直线MN对称，
∴△ABC≌△A′B′C′，且MN是线段AA′的垂直平分线，
∴∠B=∠B′，BC=B'C′，故A，D都正确，C错误；
又∵点P是直线MN上一点，
∴PA=PA′，故B正确，
故选：C．
点评 本题主要考查了轴对称的性质以及线段垂直平分线的性质的运用，解题时注意：如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
如图，△ABC与△A1B1C1是位似图形．
1．
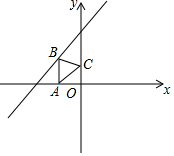如图，已知点A（-1，0），点B是直线y=x+2上的动点，点C是y轴上的动点，则△ABC的周长的最小值等于（ ）
如图，已知点A（-1，0），点B是直线y=x+2上的动点，点C是y轴上的动点，则△ABC的周长的最小值等于（ ）| A． | $\sqrt{10}$ | B． | 2+$\sqrt{2}$ | C． | 1-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{3}$ | D． | 1-$\frac{\sqrt{2}+\sqrt{5}}{2}$ |
如图，一次函数y=（m-5）x+6-2m的图象与x轴，y轴相交于A，B两点，则m的取值范围3＜m＜5．
如图，在△ABC中，AD⊥BC，∠B=45°，∠C=30°，AD=1．
某市为鼓励市民节约用水，自来水公司按分段收费标准收费，如图反映的是每月水费y（元）与用水量x（吨）之间的函数关系．
20．下列叙述中，正确的是（ ）
| A． | 相等的两个角是对顶角 | |
| B． | 老师测量跳远成绩的依据是两点之间，线段最短 | |
| C． | 从直线外一点到这条直线上的各点所连接的线段中，垂线段最短 | |
| D． | 一个角一定不等于它的余角 |