题目内容
15. 如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1.
如图,在△ABC中,AD⊥BC,∠B=45°,∠C=30°,AD=1.(1)求CD的长;
(2)求△ABC的面积.
分析 (1)由已知条件易求AC的长,再根据勾股定理即可求出CD的长;
(2)首先求出BD的长,结合(1)即可得到BC的长,由三角形面积公式计算即可.
解答 解:
(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠C=30°,AD=1,
∴AC=2AD=2,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{3}$;
(2)∵∠B=45°,
∴∠BAD=45°,
∴BD=AD=1,
∴BC=BD+CD=1+$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$AD•BC=$\frac{1+\sqrt{3}}{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
6.下列四个判断,其中错误的是( )
| A. | 数字0也是单项式 | B. | 单项式a的系数与次数都是1 | ||
| C. | $\frac{1}{2}$x2y2是二次单项式 | D. | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ |
10. 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )| A. | ∠B=∠B′ | B. | PA=PA′ | ||
| C. | BC=AA′ | D. | MN是线段AA′的垂直平分线 |
 如图,将△ABC绕点B顺时针旋转到△EBD的位置,且BA∥DE,DE的延长线交BC于点F,若BD=8,DE=6,则EF=$\frac{14}{3}$.
如图,将△ABC绕点B顺时针旋转到△EBD的位置,且BA∥DE,DE的延长线交BC于点F,若BD=8,DE=6,则EF=$\frac{14}{3}$. 已知:如图,AC∥DF,∠C=∠F,求证:BC∥EF.
已知:如图,AC∥DF,∠C=∠F,求证:BC∥EF.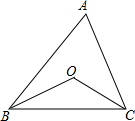 如图,已知点O是△ABC的两条角平分线的交点,
如图,已知点O是△ABC的两条角平分线的交点,