题目内容
20. 如图,△ABC与△A1B1C1是位似图形.
如图,△ABC与△A1B1C1是位似图形.(1)在网格上建立平面直角坐标系,使得点A的坐标为(-6,-1),点C1的坐标为(-3,2),则点B的坐标为(-2,-5);
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为(-2,1),计算四边形ABCP的周长为6$\sqrt{2}$+4$\sqrt{5}$.
分析 (1)直接利用已知点位置得出B点坐标即可;
(2)直接利用位似图形的性质得出对应点位置进而得出答案;
(3)直接利用位似图形的性质得出对应点交点即可位似中心,再利用勾股定理得出四边形ABCP的周长.
解答 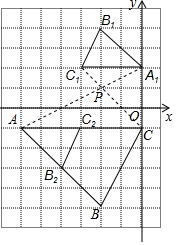 解:(1)如图所示:点B的坐标为:(-2,-5);
解:(1)如图所示:点B的坐标为:(-2,-5);
故答案为:(-2,-5);
(2)如图所示:△AB2C2,即为所求;
(3)如图所示:P点即为所求,P点坐标为:(-2,1),
四边形ABCP的周长为:$\sqrt{{4}^{2}+{4}^{2}}$+$\sqrt{{2}^{2}+{4}^{2}}$+$\sqrt{{2}^{2}+{2}^{2}}$+$\sqrt{{2}^{2}+{4}^{2}}$=4$\sqrt{2}$+2$\sqrt{5}$+2$\sqrt{2}$+2$\sqrt{5}$=6$\sqrt{2}$+4$\sqrt{5}$.
故答案为:6$\sqrt{2}$+4$\sqrt{5}$.
点评 此题主要考查了位似变换以及勾股定理,正确利用位似图形的性质分析是解题关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
9.已知二次函数y=x2经过两点(x1,y1),(x2,y2),当|x1|>|x2|时,y1,y2的大小关系是( )
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
10. 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )| A. | ∠B=∠B′ | B. | PA=PA′ | ||
| C. | BC=AA′ | D. | MN是线段AA′的垂直平分线 |
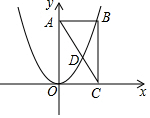 如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$. 如图,将△ABC绕点B顺时针旋转到△EBD的位置,且BA∥DE,DE的延长线交BC于点F,若BD=8,DE=6,则EF=$\frac{14}{3}$.
如图,将△ABC绕点B顺时针旋转到△EBD的位置,且BA∥DE,DE的延长线交BC于点F,若BD=8,DE=6,则EF=$\frac{14}{3}$. 如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)
如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)