题目内容
18．解不等式组$\left\{\begin{array}{l}{2（x-1）≥x+1…①}\\{\frac{x+2}{3}＞x-4…②}\end{array}\right.$，并把解集在数轴上表示出来．
分析 分别求出不等式组中两不等式的解集，找出解集的公共部分即可．
解答 解：由①得：x≥3；
由②得：x＜7，
∴不等式组的解集为3≤x＜7，
解集表示在数轴上为：
点评 此题考查了解一元一次不等式组，以及在数轴上变形不等式的解集，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
9．已知二次函数y=x2经过两点（x1，y1），（x2，y2），当|x1|＞|x2|时，y1，y2的大小关系是（ ）
| A． | y1=y2 | B． | y1＞y2 | C． | y1＜y2 | D． | 无法确定 |
6．下列四个判断，其中错误的是（ ）
| A． | 数字0也是单项式 | B． | 单项式a的系数与次数都是1 | ||
| C． | $\frac{1}{2}$x2y2是二次单项式 | D． | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ |
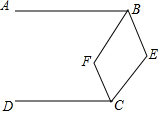如图，AB∥CD，E为直线BC右侧一点，连接BE、CE，作∠ABE和∠DCE的角平分线BF、CF相交于点F．
已知：如图，AC∥DF，∠C=∠F，求证：BC∥EF．
10．
如图，已知△ABC和△A′B′C′关于直线MN对称，点P是直线MN上一点，连接PA、PA′、AA′，下列结论错误的是（ ）
如图，已知△ABC和△A′B′C′关于直线MN对称，点P是直线MN上一点，连接PA、PA′、AA′，下列结论错误的是（ ）| A． | ∠B=∠B′ | B． | PA=PA′ | ||
| C． | BC=AA′ | D． | MN是线段AA′的垂直平分线 |
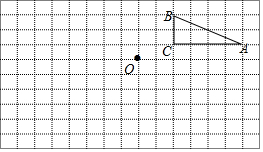如图，在边长为1个单位长度的小正方形组成的网格中，点A，B，C，O都在格点上．