题目内容
4.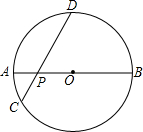 如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.
如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.
分析 分类讨论(1)P点与O点重合时,PC=PD=R,证得PC2+PD2=2R2;(2)P与O不重合时,连接OD,作OE⊥CD于E,根据垂径定理得到DE=$\frac{1}{2}$CD,根据勾股定理得到CD2=4R2-2OP2,根据相交弦定理得到PC•PD=R2-OP2,运用完全平方公式计算得到PC2+PD2=2R2.
解答 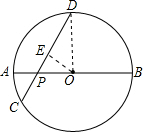 证明:设⊙O的半径为R,
证明:设⊙O的半径为R,
当点p与O点重合时,PC=PD=R,
∴PC2+PD2=2R2
当点P为一般情况时,
连接OD,作OE⊥CD于E,
则DE=$\frac{1}{2}$CD,
∴CD2=4DE2=4(R2-OE2),
∵∠APD=45°,
∴OE=$\frac{\sqrt{2}}{2}$OP,
∴CD2=4DE2=4(R2-$\frac{1}{2}$OP2)=4R2-2OP2,
∵PC•PD=PB•PA=(R-OP)(R+OP)=R2-OP2,
PC2+PD2=(PC+PD)2-2PC•PD
=4R2-2OP2-2(R2-OP2)
=2R2.
∴当点P的位置变化时,PC2+PD2的值不变化,等于圆O的半径的平方.
点评 本题考查了在圆中构建三角形运用勾股定理解直角三角形,本题中求证PC2+PD2=2OC2是解题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
15. 如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2015m停下,则这个微型机器人停在( )
如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2015m停下,则这个微型机器人停在( )
 如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2015m停下,则这个微型机器人停在( )
如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2015m停下,则这个微型机器人停在( )| A. | 点A处 | B. | 点B处 | C. | 点C处 | D. | 点E处 |
9.已知方程(m-1)x2+3x=1是关于x的一元二次方程,则m的取值范围是( )
| A. | m≠1 | B. | m≥0 | C. | m≥0且m≠1 | D. | m为任意数 |
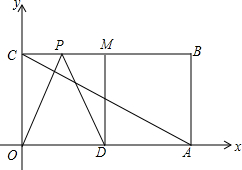 如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为(10,0)、(0,4).
如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为(10,0)、(0,4).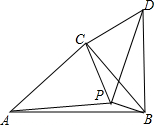 如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点且PA=3,PB=1,PC=CD=2,CD⊥PC.
如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点且PA=3,PB=1,PC=CD=2,CD⊥PC.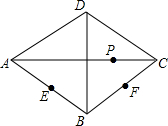 如图,菱形ABCD中,P为对角线AC上一动点,E,F分别为AB、BC中点,若AC=8,BD=6,则PE+PF的最小值为5.
如图,菱形ABCD中,P为对角线AC上一动点,E,F分别为AB、BC中点,若AC=8,BD=6,则PE+PF的最小值为5.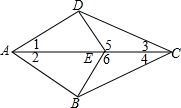 如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,
如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,