题目内容
16.计算(1)(x-3)2-9=0.
(2)(x+1)(2-x)=1.
分析 (1)先移项,然后利用直接开平方法解方程;
(2)将原方程转化为一般式方程,然后利用公式法解答.
解答 解:(1)由原方程,得
(x-3)2=9,
x-3=±3,
解得x1=6,x2=0;
(2)由原方程,得
x2-x-1=0,
∵a=1,b=-1,c=-1,
∴△=b2-4ac=(-1)2-4×1×(-1)=5
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{1±\sqrt{5}}{2}$.
点评 本题考查了解一元二次方程的方法,当把方程通过移项把等式的右边化为0后方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.当化简后不能用分解因式的方法即可考虑求根公式法,此法适用于任何一元二次方程.

练习册系列答案
相关题目
11.已知a:b:c=2:3:4,则$\frac{a-b+c}{b}$的值( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | -1 | D. | $\frac{1}{2}$或-1 |
8.(-1)2002=( )
| A. | 1 | B. | -1 | C. | -2002 | D. | 2002 |
6.计算(-x2y3)3•(-xy2)的结果是( )
| A. | -x7y11 | B. | x7y11 | C. | x6y8 | D. | -x7y8 |
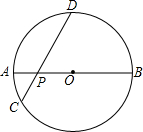 如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.
如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.