题目内容
14.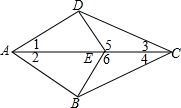 如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,
如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,求证:∠5=∠6.
分析 根据ASA推出△ADC≌△ABC,根据全等三角形的性质求出AD=BC,根据SAS推出△DCE≌△BCE,根据全等三角形的性质得出即可.
解答 证明:∵在△ADC和△ABC中
$\left\{\begin{array}{l}{∠1=∠2}\\{AC=AC}\\{∠3=∠4}\end{array}\right.$
∴△ADC≌△ABC(ASA),
∴DC=BC,
在△DCE和△BCE中
$\left\{\begin{array}{l}{DC=BC}\\{∠3=∠4}\\{CE=CE}\end{array}\right.$
∴△DCE≌△BCE(SAS),
∴∠5=∠6.
点评 本题考查了全等三角形的性质和判定的应用,能综合运用全等三角形的性质和判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.计算(-x2y3)3•(-xy2)的结果是( )
| A. | -x7y11 | B. | x7y11 | C. | x6y8 | D. | -x7y8 |
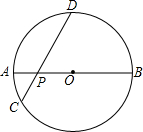 如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.
如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.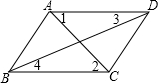 如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( ) 如图,如果△ABC≌△DEF,△DEF的周长是32cm,DE=12cm,EF=13cm,则AC=7cm.
如图,如果△ABC≌△DEF,△DEF的周长是32cm,DE=12cm,EF=13cm,则AC=7cm.