题目内容
14.我们都知道无限不循环小数是无理数,而无限循环小数是可以化成分数的.例如0.333…(3为循环节)是可以化成分数的,方法如下:令a=0.333…①
则10a=3.333…②
②-①得10a-a=3
9a=3
$a=\frac{1}{3}$
所以0.333…可以化成分数为$\frac{1}{3}$
请你阅读上面材料完成下列问题:
(1)0.$\stackrel{•}{7}$化成分数是$\frac{7}{9}$.
(2)请你将0.$\stackrel{•}{2}\stackrel{•}{6}$化为分数.
(3)请你将0.12111…(即0.12$\stackrel{•}{1}$)化为分数.
分析 (1)设0.777…=m,方程两边都乘以10,转化为7+m=10m,求出其解即可.
(2)令c=0.262626,则方程两边都乘以100,转化为100c-c=26,求出其解即可.
(3)d=0.1111…①,则10d=1.111…②,②-①得:10d-d=1,所以0.12111…=0.1111+0.01.
解答 解:(1)令b=0.777…①
则10b=7.777…②
②-①得10b-b=7,
即9b=7,解得:b=$\frac{7}{9}$,
故0.$\stackrel{•}{7}$化成分数是$\frac{7}{9}$;
(2)令c=0.262626…①
则100c=26.262626…②
②-①得100c-c=26,
即99c=26,解得:c=$\frac{26}{99}$,
故将0.$\stackrel{•}{2}\stackrel{•}{6}$化成分数为$\frac{26}{99}$;
(3)∵0.12111…=0.1111+0.02,
∴设d=0.1111…①,
则10d=1.111…②,
②-①得:10d-d=1,
即9d=1,
解得:d=$\frac{1}{9}$,
则0.12111…=0.1111+0.01=$\frac{1}{9}$+$\frac{1}{100}$=$\frac{109}{900}$.
故答案是:(1)$\frac{7}{9}$;(2)$\frac{26}{99}$;(3)$\frac{109}{900}$.
点评 本题考查了一元一次方程的应用,解答本题的关键是读懂题目所给的信息,按照题目中的运算方法求解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
4.在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{1}{2}$,则S△ABC=( )
| A. | 30 | B. | 40 | C. | 10$\sqrt{5}$ | D. | 20 |
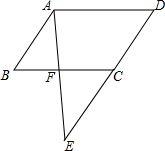 已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求:
已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求: 把下列各数在数轴上表示,并从小到大的顺序用“<”连接起来.
把下列各数在数轴上表示,并从小到大的顺序用“<”连接起来.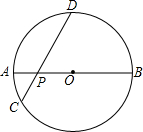 如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.
如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.