题目内容
12.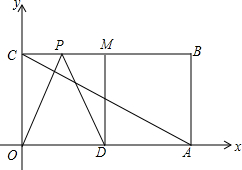 如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为(10,0)、(0,4).
如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为(10,0)、(0,4).(1)求线段AC的长及AC的中点坐标;
(2)点D是0A的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,求点P的坐标.
分析 (1)根据勾股定理即可求出AC的长,由点点A、C的坐标分别为(10,0)、(0,4)即可求出AC中点的坐标;
(2)分OP=OD、PD=OD和PO=PD三种情况,结合矩形的性质和勾股定理可求得P点的坐标.
解答 解:(1)∵四边形OABC是长方形,
∴∠AOC=90°,
∵点A、C的坐标分别为(10,0)、(0,4),
∴OC=4,OA=10,
∴AC=$\sqrt{1{0}^{2}+{4}^{2}}$=2$\sqrt{29}$,AC的中点坐标是(5,2);
(2)∵A(10,0),C(0,4),且四边形OABC是矩形,
∴OA=BC=10,OC=AB=4,
∵D是OA的中点,
∴OD=5,
当△ODP是腰长为5的等腰三角形时,则有PO=OD=5、PD=OD=5或PO=PD=5,
当PO=OD=5时,在Rt△OPC中,OC=4,OP=5,由勾股定理可求得PC=3,此时P点坐标为(3,4);
当PD=OD=5时,过P作PE⊥OA于点E,如图1,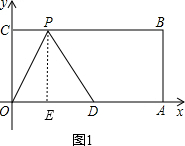
在Rt△PED中,PE=OC=4,PD=5,由勾股定理可求得DE=3,且OD=5,则OE=5-3=2,此时P点坐标为(2,4);
当PO=PD=5时,过P作PF⊥OA于点F,如图2,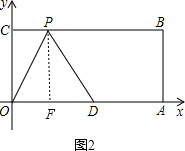
在Rt△POF中,PF=4,PO=5,由勾股定理可求得OF=3,则OD=6,与已知矛盾,故该情况不存在;
综上可知点P的坐标为(3,4)或(2,4).
点评 此题主要考查了矩形的性质以及坐标与图形的性质和等腰三角形的性质,根据△ODP是腰长为5的等腰三角形进行分类讨论是解决问题的关键.

练习册系列答案
相关题目
17.香蕉每千克m元,买10千克以上9折优惠(即按原价的90%出售),买20千克应付( )
| A. | 20m元 | B. | 20×90%m元 | C. | 20×(1+90%)m元 | D. | 20×(1-90%)m元 |
 如图.矩形ABCD的顶点B,C在坐标轴上,顶点D的坐标是(3,3),若直线y=mx恰好将矩形分成面积相等的两部分,求m的值.
如图.矩形ABCD的顶点B,C在坐标轴上,顶点D的坐标是(3,3),若直线y=mx恰好将矩形分成面积相等的两部分,求m的值.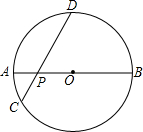 如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.
如图,AB是半径为R的⊙O的直径,P为直径AB上的一动点,过P作弦CD,且∠DPB=45°,则当点P的位置变化时,PC2+PD2的值是否变化?若不变,请求出这个定值?若变化,请说明理由.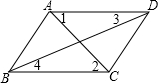 如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )