题目内容

19．如图，四边形ABCD中，从①AB∥CD；②AB=CD；③BC∥AD；④BC=AD四项中任意选两个作为条件，则下列选项中不能判定四边形ABCD是平行四边形的是（　　）
A．①②B．②③C．①③D．③④

分析 根据平行四边形的判定方法逐一进行选择判断．

解答 解：A、由一组对边平行且相等的四边形是平行四边形，能推导出四边形ABCD是平行四边形，故本选项正确；
B、一组对边平行而另一组对边相等不能推导出四边形ABCD是平行四边形，故本选项错误；
C、两组对边分别平行的四边形是平行四边形，能推导出四边形ABCD是平行四边形，故本选项正确；
D、由一组对边平行且相等的四边形是平行四边形，能推导出四边形ABCD是平行四边形，故本选项正确；
故选B．

点评 本题考查了平行四边形的判定，属于基础题型，关键要记准平行四边形的判定方法．

练习册系列答案
相关题目
9．如图1，在四边形ABCD中，AD∥BC，∠C=90°，CD=8cm，动点P，Q同时从点B出发，速度都是1cm/s，点P沿BA，AD，DC运动到点C停止，点Q沿BC运动到点C停止．当点P运动到点A时，点Q恰好运动到点C．设点P运动的时间为t（s）（t≥0）时，△BPQ的面积为y（cm2）．已知点P在AD边上运动时y与t的函数图象是图2中的线段MN．则点P在BA边上运动时，y与t的函数关系式（注明自变量的取值范围）为y=$\frac{2}{5}$t2（0≤t≤10）．
10．如图，矩形ABCD中，AD=5，AB=7，点E为DC上一个动点，把△ADE沿AE折叠，点D的对应点为D′，若D′落在∠ABC的平分线上时，DE的长为（　　）
A．3或4B．$\frac{5}{2}$或$\frac{5}{3}$C．$\frac{5}{2}$或$\frac{3}{5}$D．$\frac{2}{5}$或$\frac{5}{3}$
7．下列命题是真命题的是（　　）
A．如果两角是同位角，那么这两角一定相等
B．两互补的角一定是邻补角
C．如果a2=b2，那么a=b
D．如果两个角不相等，那么这两个角不是对顶角
14．当x≠1时分式$\frac{1+x}{1-x}$有意义；当x=-3时分式$\frac{{{x^2}-9}}{x-3}$的值为零．
4．甲、乙、丙、丁四名射手在预选赛中所得的平均环数$\overline{x}$及其方差s2如表所示，则选拔 一名参赛的人选，应是（　　）
 甲乙丙丁
 $\overline{x}$ 7 8 87
 s2 6.3 6.3 78.7
A．甲B．乙C．丙D．丁
11．在一次射击训练中，甲、乙两人前5次射击的成绩（单位：环）如下：
甲：10  8  10  10  7         乙：7  10  9  9  10
在这次练习中，甲、乙两人成绩的方差关系是（　　）
A．.甲 大于乙B．.甲小于乙C．.甲等于乙D．无法确定
8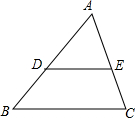．如图，点D、E分别在△ABC的边AB、AC上，下列条件不能使△ADE∽△ABC相似的是（　　）
A．DE∥BCB．AD：AB=DE：BCC．AD：DB=AE：ECD．∠BDE+∠DBC=180°
9．如图1，已知在平行四边形ABCD中，AB=5，BC=8，cosB=$\frac{4}{5}$，点P是边BC上的动点，以CP为半径的圆C与边AD交于点E、F（点F在点E的右侧），射线CE与射线BA交于点G．
（1）当圆C经过点A时，求CP的长；
（2）如图2，连接AP，当AP∥CG时，求弦EF的长；
（3）如图3，当BC=BG时，求圆C的半径长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网