题目内容
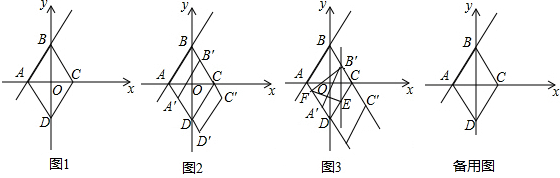
10. 如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′,若D′落在∠ABC的平分线上时,DE的长为( )
如图,矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′,若D′落在∠ABC的平分线上时,DE的长为( )| A. | 3或4 | B. | $\frac{5}{2}$或$\frac{5}{3}$ | C. | $\frac{5}{2}$或$\frac{3}{5}$ | D. | $\frac{2}{5}$或$\frac{5}{3}$ |
分析 连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P,先利用勾股定理求出MD′,再分两种情况利用勾股定理求出DE.
解答 解:如图,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P
∵点D的对应点D′落在∠ABC的角平分线上,
∴MD′=PD′,
设MD′=x,则PD′=BM=x,
∴AM=AB-BM=7-x,
又折叠图形可得AD=AD′=5,
∴x2+(7-x)2=25,解得x=3或4,
即MD′=3或4.
在Rt△END′中,设ED′=a,
①当MD′=3时,AM=7-3=4,D′N=5-3=2,EN=4-a,
∴a2=22+(4-a)2,
解得a=$\frac{5}{2}$,即DE=$\frac{5}{2}$,
②当MD′=4时,AM=7-4=3,D′N=5-4=1,EN=3-a,
∴a2=12+(3-a)2,
解得a=$\frac{5}{3}$,即DE=$\frac{5}{3}$.
故选B.
点评 本题主要考查了折叠问题,解题的关键是明确掌握折叠以后有哪些线段是对应相等的.

练习册系列答案
相关题目
18.若分式$\frac{x-3}{x}$的值为负数,则x的取值范围是( )
| A. | x>3 | B. | 0<x<3 | C. | x<3且x≠0 | D. | x>-3且x≠0 |
19. 如图,四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD四项中任意选两个作为条件,则下列选项中不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD四项中任意选两个作为条件,则下列选项中不能判定四边形ABCD是平行四边形的是( )
 如图,四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD四项中任意选两个作为条件,则下列选项中不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD四项中任意选两个作为条件,则下列选项中不能判定四边形ABCD是平行四边形的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
20.下列是勾股数的是( )
| A. | 30 40 50 | B. | 1 2 3 | C. | 4 12 13 | D. | 5 6 7 |
 如图,直线l1:y=-x+8与x轴、y轴分别交于点A和点B,直线l2:y=x与直线l1交于点C,D为线段BC上一点,点D从B出发,以每秒$\sqrt{2}$个单位长度沿BC方向运动,到C点时停止.过D作直线DP垂直于x轴,交线段OC、x轴于点E,P,以DE为斜边向左侧等腰Rt△DEF,点D的运动时间为t(秒)
如图,直线l1:y=-x+8与x轴、y轴分别交于点A和点B,直线l2:y=x与直线l1交于点C,D为线段BC上一点,点D从B出发,以每秒$\sqrt{2}$个单位长度沿BC方向运动,到C点时停止.过D作直线DP垂直于x轴,交线段OC、x轴于点E,P,以DE为斜边向左侧等腰Rt△DEF,点D的运动时间为t(秒) 在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张卡片(大小、颜色、形状相同)的正面上分别写有如下四个等式中的一个等式:①AB=CD;②AD∥BC;③AB∥CD;④∠A=∠C;小英同学闭上眼睛从四张卡片中随机抽出一张,再从剩下的卡片中随机抽出另一张,请结合图形回答下列问题:
在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张卡片(大小、颜色、形状相同)的正面上分别写有如下四个等式中的一个等式:①AB=CD;②AD∥BC;③AB∥CD;④∠A=∠C;小英同学闭上眼睛从四张卡片中随机抽出一张,再从剩下的卡片中随机抽出另一张,请结合图形回答下列问题: