题目内容
2.若|ab-2|+|b-1|=0,试求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+…+$\frac{1}{(a+2015)(b+2015)}$的值.分析 由非负数的性质求得a、b的值,然后利用拆项裂项法求得代数式的值即可.
解答 解:∵|ab-2|+|b-1|=0,
∴b=1,a=2.
∴原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$
=1$-\frac{1}{2}$$+\frac{1}{2}$$-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+$…+$\frac{1}{2016}-\frac{1}{2017}$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$.
点评 本题主要考查的是非负数的性质,利用拆项裂项法求解是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
12. 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A=∠2 | B. | ∠1=∠2 | C. | ∠A与∠D互为余角 | D. | △ABC≌△CED |
13.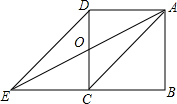 如图,延长正方形ABCD的边BC至点E,使得CE=BC,连接AC,DE,AE与CD交于点0,则下列结论中一定不成立的是( )
如图,延长正方形ABCD的边BC至点E,使得CE=BC,连接AC,DE,AE与CD交于点0,则下列结论中一定不成立的是( )
 如图,延长正方形ABCD的边BC至点E,使得CE=BC,连接AC,DE,AE与CD交于点0,则下列结论中一定不成立的是( )
如图,延长正方形ABCD的边BC至点E,使得CE=BC,连接AC,DE,AE与CD交于点0,则下列结论中一定不成立的是( )| A. | AC∥DE | B. | △OCE旋转180°会与△ODA完全重合 | ||
| C. | 若AB=1,则OA=$\frac{\sqrt{5}}{2}$ | D. | ∠AEB=30° |
7.在$\frac{ab}{2}$、$\frac{x(x-3)}{2x}$、$\frac{5+x}{π-1}$、$\frac{a+b}{a-2b}$、x+$\frac{1}{x}$中,是分式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.解方程:
(1)$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
(2)$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$.
(1)$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
(2)$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$.
11. 将量角器按如图摆放在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
将量角器按如图摆放在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
 将量角器按如图摆放在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
将量角器按如图摆放在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )| A. | 15° | B. | 28° | C. | 30° | D. | 56° |