题目内容
12. 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A=∠2 | B. | ∠1=∠2 | C. | ∠A与∠D互为余角 | D. | △ABC≌△CED |
分析 先根据角角边证明△ABC与△CED全等,再根据全等三角形对应边相等,全等三角形的对应角相等的性质对各选项判断后,利用排除法求解.
解答 解:∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
$\left\{\begin{array}{l}{∠B=∠E=9{0}^{°}}\\{∠A=∠2}\\{AC=CD}\end{array}\right.$,
∴△ABC≌△CED(AAS),
故A、D选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故C选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=90°,
故B选项错误.
故选B.
点评 本题主要考查全等三角形的性质,先证明三角形全等是解决本题的突破口,也是难点所在.做题时,要结合已知条件与全等的判定方法对选项逐一验证.

练习册系列答案
相关题目
4.在下列方程中是一元二次方程的是( )
| A. | x2-2xy+y2=0 | B. | mx2-2x=x2+1 | C. | x2-2x=-3 | D. | ax2+bx+c=0 |
1.若二次函数y=(m+1)x2-mx+m2-2m-3的图象经过原点,则m的值必为( )
| A. | -1或3 | B. | -1 | C. | 3 | D. | -3或1 |
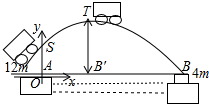 著名艺人柯受良于2003年12月9日在上海不幸去世,柯受良生前以飞车特技著称,曾经飞越过长城,黄河等,多年前,柯受良驾车飞越黄河的壮举令所有中国人为之骄傲,现在请你来解答其中的数学问题.如图,设黄河的两岸处于同一水平线上,汽车飞越的水平距离AB是41m,起飞高度OS为12m,落地点B(汽车落在一堆软箱中)的高度是4m,建立如图所示的坐标系,在某起飞角度,汽车飞越的路径为抛物线y=-$\frac{5}{v^2}$x2+$\frac{1}{5}$x+h.(其中v为汽车的起飞速度,单位:m/s;h为常数,h,x,y的单位:m)
著名艺人柯受良于2003年12月9日在上海不幸去世,柯受良生前以飞车特技著称,曾经飞越过长城,黄河等,多年前,柯受良驾车飞越黄河的壮举令所有中国人为之骄傲,现在请你来解答其中的数学问题.如图,设黄河的两岸处于同一水平线上,汽车飞越的水平距离AB是41m,起飞高度OS为12m,落地点B(汽车落在一堆软箱中)的高度是4m,建立如图所示的坐标系,在某起飞角度,汽车飞越的路径为抛物线y=-$\frac{5}{v^2}$x2+$\frac{1}{5}$x+h.(其中v为汽车的起飞速度,单位:m/s;h为常数,h,x,y的单位:m)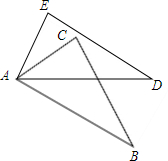 如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.
如图所示,AB=AD,AC=AE,BC=DE,如果∠EAD=70°,∠CAD=40°,求∠BAD的度数.