题目内容
13.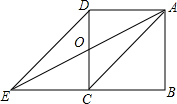 如图,延长正方形ABCD的边BC至点E,使得CE=BC,连接AC,DE,AE与CD交于点0,则下列结论中一定不成立的是( )
如图,延长正方形ABCD的边BC至点E,使得CE=BC,连接AC,DE,AE与CD交于点0,则下列结论中一定不成立的是( )| A. | AC∥DE | B. | △OCE旋转180°会与△ODA完全重合 | ||
| C. | 若AB=1,则OA=$\frac{\sqrt{5}}{2}$ | D. | ∠AEB=30° |
分析 由正方形的性质和已知条件证出四边形ADEC是平行四边形,得出AC∥DE,OA=OE,OC=OD,A、B一定成立;若AB=1,由勾股定理求出AE,得出OA=$\frac{1}{2}$AE=$\frac{\sqrt{5}}{2}$,得出C一定成立;由三角函数tan∠AEB=$\frac{AB}{BE}$=$\frac{1}{2}$,得出∠AEB≠30°,D一定不成立;即可得出结论.
解答 解:∵四边形ABCD是正方形,
∴AD=BC=CD=AB,AD∥BC,∠B=90°,
∵CE=BC,
∴CE=AD,
∴四边形ADEC是平行四边形,
∴AC∥DE,OA=OE,OC=OD,
∴△OCE旋转180°会与△ODA重合,
∴A、B一定成立;
若AB=1,则BC=CE=AB=1,
∴AE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴OA=$\frac{1}{2}$AE=$\frac{\sqrt{5}}{2}$,
∴C一定成立;
∵tan∠AEB=$\frac{AB}{BE}$=$\frac{1}{2}$,
∴∠AEB≠30°,
∴D一定不成立.
故选:D.
点评 本题考查了正方形的性质、平行四边形的判定与性质、勾股定理、三角函数等知识;熟练掌握正方形的性质,证明四边形是平行四边形是解决问题的关键.

练习册系列答案
相关题目
4.在下列方程中是一元二次方程的是( )
| A. | x2-2xy+y2=0 | B. | mx2-2x=x2+1 | C. | x2-2x=-3 | D. | ax2+bx+c=0 |
1.若二次函数y=(m+1)x2-mx+m2-2m-3的图象经过原点,则m的值必为( )
| A. | -1或3 | B. | -1 | C. | 3 | D. | -3或1 |
5.已知三角形的两条边长分别为1、1,则第三条边长可能是( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
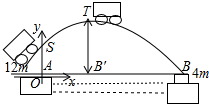 著名艺人柯受良于2003年12月9日在上海不幸去世,柯受良生前以飞车特技著称,曾经飞越过长城,黄河等,多年前,柯受良驾车飞越黄河的壮举令所有中国人为之骄傲,现在请你来解答其中的数学问题.如图,设黄河的两岸处于同一水平线上,汽车飞越的水平距离AB是41m,起飞高度OS为12m,落地点B(汽车落在一堆软箱中)的高度是4m,建立如图所示的坐标系,在某起飞角度,汽车飞越的路径为抛物线y=-$\frac{5}{v^2}$x2+$\frac{1}{5}$x+h.(其中v为汽车的起飞速度,单位:m/s;h为常数,h,x,y的单位:m)
著名艺人柯受良于2003年12月9日在上海不幸去世,柯受良生前以飞车特技著称,曾经飞越过长城,黄河等,多年前,柯受良驾车飞越黄河的壮举令所有中国人为之骄傲,现在请你来解答其中的数学问题.如图,设黄河的两岸处于同一水平线上,汽车飞越的水平距离AB是41m,起飞高度OS为12m,落地点B(汽车落在一堆软箱中)的高度是4m,建立如图所示的坐标系,在某起飞角度,汽车飞越的路径为抛物线y=-$\frac{5}{v^2}$x2+$\frac{1}{5}$x+h.(其中v为汽车的起飞速度,单位:m/s;h为常数,h,x,y的单位:m)