题目内容
14．解方程：（1）$\frac{x}{x-2}-\frac{2}{{x}^{2}-4}=1$
（2）$\frac{3}{x}-\frac{2}{1-x}=\frac{x+5}{{x}^{2}-x}$．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）去分母得：x2+2x-2=x2-4，
解得：x=-1，
经检验x=-1是分式方程的解；
（2）去分母得：3x-3+2x=x+5，
解得：x=2，
经检验x=2是增根，分式方程无解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
优加精卷系列答案
相关题目
4．在下列方程中是一元二次方程的是（ ）
| A． | x2-2xy+y2=0 | B． | mx2-2x=x2+1 | C． | x2-2x=-3 | D． | ax2+bx+c=0 |
5．已知三角形的两条边长分别为1、1，则第三条边长可能是（ ）
| A． | -1 | B． | 1 | C． | 2 | D． | 3 |
9．下列各式中，最简分式是（ ）
| A． | $\frac{34（x+y）}{85（x-y）}$ | B． | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}y+x{y}^{2}}$ | ||
| C． | $\frac{{y}^{2}{-x}^{2}}{x+y}$ | D． | $\frac{（x+y）^{2}}{{y}^{2}-{x}^{2}}$ |
19．方程x2-4x-m2=0根的情况是（ ）
| A． | 一定有两不等实数根 | B． | 一定有两相等实数根 | ||
| C． | 一定无实数根 | D． | 根的情况不确定 |
6．（x2+y2）2-4（x2+y2）-5=0，则x2+y2的值为（ ）
| A． | 5 | B． | -1 | C． | 5或-1 | D． | 无法确定 |
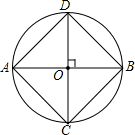如图，AB、CD是⊙O的两条互相垂直的直径．