题目内容
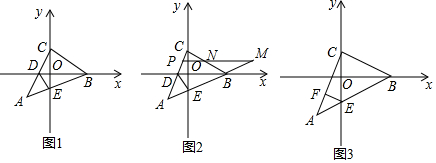
12. 已知:如图,在山脚的C处测得山顶A的仰角为53°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为63°,求此山的高度AB.(答案保留根号)
已知:如图,在山脚的C处测得山顶A的仰角为53°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为63°,求此山的高度AB.(答案保留根号)(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,sin63°≈$\frac{12}{13}$,cos63°≈$\frac{5}{13}$,tan63°≈$\frac{12}{5}$)
分析 首先根据题意分析图形;作DN⊥AB于N,作DM⊥BC于M,构造两个直角三角形,分别求解可得DM与AN的值,再利用图形关系,进而可求出答案.
解答  解:如图,作DN⊥AB于N,作DM⊥BC于M.
解:如图,作DN⊥AB于N,作DM⊥BC于M.
∵在Rt△CDM中,∠DCM=30°,CD=400米,
∴DM=CD•sin30°=$\frac{1}{2}$×400=200(米),
CM=CD•cos30°=$\frac{\sqrt{3}}{2}$×400=200$\sqrt{3}$(米).
∵在Rt△ADN中,∠ADN=63°,设DN=x米,
∴AN=tan63°•x=$\frac{12}{5}$x(米).
在矩形DMBN中,BN=DM=200米.
∵在Rt△ACB中,∠ACB=53°,
∴tan53°=$\frac{AB}{BC}$,即:$\frac{4}{3}$=$\frac{\frac{12}{5}x+200}{x+200\sqrt{3}}$,
∴x=250$\sqrt{3}$-$\frac{375}{2}$,
∴AB=AN+BN=$\frac{12}{5}$(250$\sqrt{3}$-$\frac{375}{2}$)+200=600$\sqrt{3}$-250(米).
答:此山的高度AB为(600$\sqrt{3}$-250)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识解直角三角形,难度一般.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.某粮仓原有大米132吨,某一周该粮仓大米的进出情况如下表:(当天运进大米8 吨,记作+8吨;当天运出大米15吨,记作-15吨.)
(1)若经过这一周,该粮仓存有大米88吨,求m的值,并说明星期五该粮仓是运进还是运出大米,运进或运出大米多少吨?
(2)若大米进出库的装卸费用为每吨15元,求这一周该粮仓需要支付的装卸总费用.
| 某粮仓大米一周进出情况表(单位:吨) | ||||||
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| -32 | +26 | -23 | -16 | m | +42 | -21 |
(2)若大米进出库的装卸费用为每吨15元,求这一周该粮仓需要支付的装卸总费用.
4.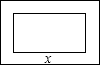 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )| A. | (50-x)(80-x)=5400 | B. | (50-2x)(80-2x)=5400 | C. | (50+x)(80+x)=5400 | D. | (50+2x)(80+2x)=5400 |
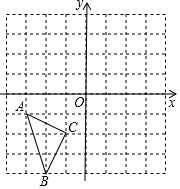 △ABC在平面直角坐标系中的位置如图所示
△ABC在平面直角坐标系中的位置如图所示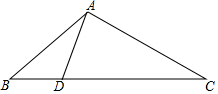 如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.
如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.