题目内容
13. 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B运动:点Q从点B开始,沿BC边以2cm/s的速度向点C运动,当点P运动到点B时,运动停止,如果P、Q分别从A、B两点同时出发.
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B运动:点Q从点B开始,沿BC边以2cm/s的速度向点C运动,当点P运动到点B时,运动停止,如果P、Q分别从A、B两点同时出发.(1)几秒后△PBQ的面积等于8cm2?
(2)几秒后以P、B、Q为顶点的三角形与△ABC相似?
分析 (1)设t秒后△PBQ的面积等于8cm,此时,AP=t,BP=6-t,BQ=2t,再由三角形的面积公式即可得出结论;
(2)设x秒后以P、B、Q为顶点的三角形与△ABC相似,此时,AP=x,BP=6-x,BQ=2x,再分△BPQ∽△BAC与△BPQ∽△BCA两种情况进行讨论即可.
解答 解:(1)设t秒后△PBQ的面积等于8cm,此时,AP=t,BP=6-t,BQ=2t,
∵S△PBQ=$\frac{1}{2}$BP•BQ,即$\frac{1}{2}$(6-t)×2t=8,即t2+6t+8=0,解得t1=2,t2=4.
∴2秒或4秒后,△PBQ的面积等于8cm2;
(2)设x秒后以P、B、Q为顶点的三角形与△ABC相似,此时,AP=x,BP=6-x,BQ=2x,
①若△BPQ∽△BAC,则$\frac{BP}{BA}$=$\frac{BQ}{BC}$,即$\frac{6-x}{6}$=$\frac{2x}{12}$,解得x=3;
②若△BPQ∽△BCA,则$\frac{BP}{BC}$=$\frac{BQ}{BA}$,即$\frac{6-x}{12}$=$\frac{2x}{6}$,解得x=1.2.
综上所述,1.2秒或3秒后,以P、B、Q为顶点的三角形与△ABC相似.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
4.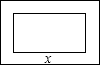 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )| A. | (50-x)(80-x)=5400 | B. | (50-2x)(80-2x)=5400 | C. | (50+x)(80+x)=5400 | D. | (50+2x)(80+2x)=5400 |
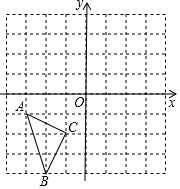 △ABC在平面直角坐标系中的位置如图所示
△ABC在平面直角坐标系中的位置如图所示