题目内容
9.某景区商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个;第二周若按每个10元的价格销售仍可售出200个,但商店为了提高销售量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出.(1)如果这批旅游纪念品共获利1050元,那么第二周每个旅游纪念品的销售价格为多少元?
(2)第二周每个旅游纪念品的销售价格为多少时,这批旅游纪念品利润最大?最大利润是多少?
分析 (1)根据纪念品的进价和售价以及销量分别表示出两周的总利润,进而得出等式求出即可;
(2)根据纪念品的进价和售价以及销量分别表示出两周的总利润,进而得出函数关系式求出即可.
解答 解:(1)由题意得:
200×(10-6)+(10-x-6)(200+50x)+(4-6)[600-200-(200+50x)]=1050,
即800+(4-x)(200+50x)-2(200-50x)=1050,
整理得:x2-2x-3=0,
解得:x1=3,x2=-1
依题意,0≤x≤6,∴x=3
10-x=10-3=7.
答:第二周的销售价格为7元.
(2)设这批旅游纪念品的利润为y元,则
y=200×(10-6)+(10-x-6)(200+50x)+(4-6)[600-200-(200+50x)]
=-50+100x+1200 (0≤x≤6)
∵a=-50<0,
∴当x=-=1(满足0≤x≤6)时,y有最大值,最大值是:=1250.
这时,10-x=10-1=9
答:第二周每个旅游纪念品的销售价格为9元时,这批旅游纪念品利润最大,最大利润是1250元.
点评 此题主要考查了一元二次方程以及二次函数的应用,根据已知表示出两周的利润是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.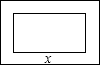 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )| A. | (50-x)(80-x)=5400 | B. | (50-2x)(80-2x)=5400 | C. | (50+x)(80+x)=5400 | D. | (50+2x)(80+2x)=5400 |
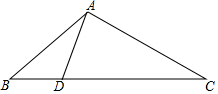 如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.
如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.
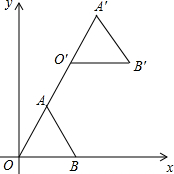 已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内
已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内
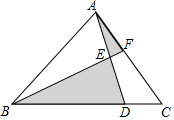 三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.
三角形ABC的面积为10cm2,AE=$\frac{1}{2}$AD,BD=3DC,求阴影部分的面积.