题目内容
16.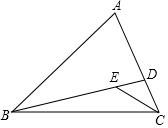 已知:如图,△ABC中,∠A=65°,∠ABD=30°,∠ACB=72°,CE平分∠ACB.
已知:如图,△ABC中,∠A=65°,∠ABD=30°,∠ACB=72°,CE平分∠ACB.求:∠CED的度数.
分析 由∠A、∠ABD的度数利用三角形外角性质即可得出∠CDE的度数,由∠ACB的度数利用角平分线的定义即可得出∠DCE的度数,再根据三角形内角和定理即可求出∠CED的度数,此题得解.
解答 解:∵∠A=65°,∠ABD=30°,
∴∠CDE=∠A+∠ABD=95°.
∵∠ACB=72°,CE平分∠ACB,
∴∠DCE=$\frac{1}{2}$∠ACB=36°,
∴∠CED=180°-∠DCE-∠CDE=180°-36°-95°=49°.
点评 本题考查了三角形内角和定理、三角形的外角性质以及角平分线的定义,熟练掌握“三角形内角和是180°”是解题的关键.

练习册系列答案
相关题目
4.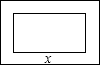 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
 在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )
在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示.设边框的宽为xcm,如果整个挂图的面积是5400cm2,那么下列方程符合题意的是( )| A. | (50-x)(80-x)=5400 | B. | (50-2x)(80-2x)=5400 | C. | (50+x)(80+x)=5400 | D. | (50+2x)(80+2x)=5400 |
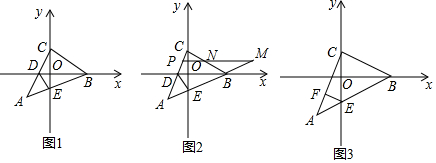
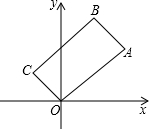 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.