题目内容
17．
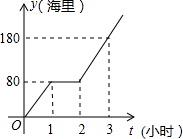我国边防海警按照计划指定海域去巡逻，某巡逻艇匀速行驶一段时间后，因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好准点到达，如图是该艇行驶的路程y（海里）与所用时间t（小时）之间的函数图象，求该巡逻艇原计划准点到达指定海域所要行驶的路程．
分析 根据图象即可得出边防海警按照计划到达指定海域所要行驶的路程．
解答 解：由图象及题意，得
故障前的速度为：80÷1=80海里/时，
故障后的速度为：（180-80）÷1=100海里/时．
设航行额全程有a海里，由题意，得
| a |
| 80 |
| a-80 |
| 100 |
解得：a=480．
故答案为：480．
点评 本题考查了运用函数图象的意义解答行程问题的运用，边防海警按照计划到达指定海域所要行驶的路程是关键．
练习册系列答案
相关题目
7．若把函数y=（x-3）2-2的图象向左平移a个单位，再向上平移b（b＞0）个单位，所得图象的函数表达式是y=（x+3）2+2，则（ ）
| A． | a=6，b=4 | B． | a=-6，b=4 | C． | a=6，b=-4 | D． | a=-6，b=-4 |
8．
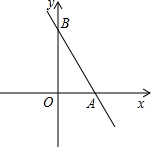直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B，M是y轴上一点，若将△ABM沿AM折叠，点B恰好落在x轴上，则点M的坐标为（0，$\frac{3}{2}$）或（0，-6）．
直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B，M是y轴上一点，若将△ABM沿AM折叠，点B恰好落在x轴上，则点M的坐标为（0，$\frac{3}{2}$）或（0，-6）． 
某通讯公司推出了①②两种收费方式，收费y1，y2 （元）与通讯时间x（分钟）之间的函数关系如图所示，则使不等式kx+30＜$\frac{1}{5}$x成立的x的取值范围是x＞300．
12．在武汉二中广雅中学举办的演讲比赛活动中，评委将学生的成绩分为A、B、C、D四个等级，并绘制了如图所示的不完整两种统计图，根据图中所提供的信息，下列说法中错误的是（ ）
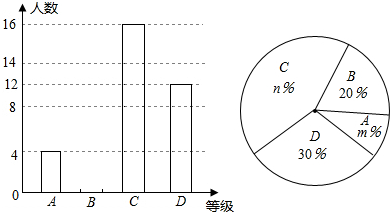
| A． | 参加演讲比赛学生共40人 | |
| B． | 扇形统计图中m=10，n=40 | |
| C． | 学校欲从获A等级的学生中随机选取2人参加市级比赛，选中A等级的小明的概率为$\frac{1}{2}$ | |
| D． | C等级所对应的圆心角为120度 |
9．一元一次不等式组$\left\{{\begin{array}{l}{2x+1＞1}\\{\frac{1}{3}x-1≤0}\end{array}}\right.$的解集在数轴上表示为（ ）
| A． |  | B． |  | C． |  | D． |  |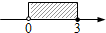
7．
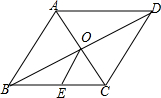如图，在菱形ABCD中，对角线AC与BD相交于点O，E为BC的中点，若BD=2$\sqrt{3}$cm，AC=2cm，则OE的长为（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，E为BC的中点，若BD=2$\sqrt{3}$cm，AC=2cm，则OE的长为（ ）| A． | $\sqrt{3}$cm | B． | 2cm | C． | 1cm | D． | $\frac{\sqrt{3}}{2}$cm |