题目内容
5. 某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.
某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.
分析 首先将已知点的坐标代入一次函数的解析式求得k值,然后确定两函数图象的交点坐标,从而确定x的取值范围.
解答 解:∵y=kx+30经过点(500,80),
∴k═$\frac{1}{10}$,
∴$\left\{\begin{array}{l}{{y}_{1=}\frac{1}{10}x+30}\\{{y}_{2=}\frac{1}{5}x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=300}\\{y=60}\end{array}\right.$,
∴两直线的交点坐标为(300,60),
∴当x>300时不等式kx+30<$\frac{1}{5}$x成立,
故答案为:x>300.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
15.从-1,0,$\frac{1}{3}$,π,$\sqrt{3}$中随机任取一数,取到无理数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.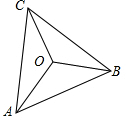 如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
 如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
10.函数y=$\sqrt{x+1}$自变量x的取值范围( )
| A. | x≥1 | B. | x≤-1 | C. | x≥-1 | D. | x≤1 |
 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法: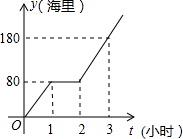 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.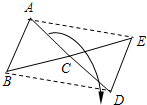 已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.
已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.