题目内容
7.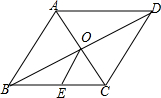 如图,在菱形ABCD中,对角线AC与BD相交于点O,E为BC的中点,若BD=2$\sqrt{3}$cm,AC=2cm,则OE的长为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,E为BC的中点,若BD=2$\sqrt{3}$cm,AC=2cm,则OE的长为( )| A. | $\sqrt{3}$cm | B. | 2cm | C. | 1cm | D. | $\frac{\sqrt{3}}{2}$cm |
分析 首先利用勾股定理求出BC的长,由菱形的四边相等即可得到BC的长,再由三角形中位线定理即可求出OE的长.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD于O,AB=BC=CD=AD,
∵BD=2$\sqrt{3}$cm,AC=2cm,
∴BO=$\sqrt{3}$,CO=1,
∴BC=CD=2,
∵E为BC的中点,
∴OE是△BOC的中位线,
∴OE=$\frac{1}{2}$CD=1cm,
故选C.
点评 本题考查了菱形的对角线互相垂直平分的性质,勾股定理的应用,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质与定理是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
18.小月的讲义夹里放了大小相同的试卷共12页,其中语文5页、数学3页、英语4页,她随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{12}$ |
19.在平面直角坐标系中,点P(m,m-2)不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.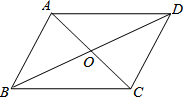 如图,平行四边形ABCD的对角线交于点O,且AB=4,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=4,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
 如图,平行四边形ABCD的对角线交于点O,且AB=4,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=4,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )| A. | 28 | B. | 32 | C. | 36 | D. | 46 |
17.长方形面积是3a2-3ab+6a,一边长为3a,则它的另一条边长为( )
| A. | 2a-b+2 | B. | a-b+2 | C. | 3a-b+2 | D. | 4a-b+2 |
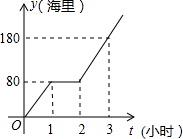 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.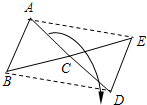 已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.
已知:如图所示,△ABC为任意三角形,若将△ABC绕点C顺时针旋转180° 得到△DEC.