题目内容
4.在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=$\frac{1}{x}$相交于点A、B,且AC+BC=4,则△OAB的面积为( )| A. | 2$\sqrt{3}$+3或2$\sqrt{3}$-3 | B. | $\sqrt{2}$+1或$\sqrt{2}$-1 | C. | 2$\sqrt{3}$-3 | D. | $\sqrt{2}$-1 |
分析 根据题意表示出AC,BC的长,进而得出等式求出m的值,进而得出答案.
解答 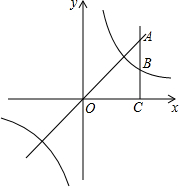 解:如图所示:设点C的坐标为(m,0),则A(m,m),B(m,$\frac{1}{m}$),
解:如图所示:设点C的坐标为(m,0),则A(m,m),B(m,$\frac{1}{m}$),
所以AC=m,BC=$\frac{1}{m}$.
∵AC+BC=4,
∴可列方程m+$\frac{1}{m}$=4,
解得:m=2±$\sqrt{3}$.
故$\frac{1}{m}$=2±$\sqrt{3}$,
所以A(2+$\sqrt{3}$,2+$\sqrt{3}$),B(2+$\sqrt{3}$,2-$\sqrt{3}$)或A(2-$\sqrt{3}$,2-$\sqrt{3}$),B(2-$\sqrt{3}$,2+$\sqrt{3}$),
∴AB=2$\sqrt{3}$.
∴△OAB的面积=$\frac{1}{2}$×2$\sqrt{3}$×(2±$\sqrt{3}$)=2$\sqrt{3}$±3.
故选:A.
点评 此题主要考查了反比例函数与一次函数的交点,正确表示出各线段长是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.$\frac{\sqrt{2}}{2}$的倒数是( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{1}{2}$ |
15.关于x的方程mx2-4x-m+5=0,有以下说法:
①当m=0时,方程只有一个实数根;②当m=1时,方程有两个相等的实数根;③当m=-1时,方程没有实数根.则其中正确的是( )
①当m=0时,方程只有一个实数根;②当m=1时,方程有两个相等的实数根;③当m=-1时,方程没有实数根.则其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
19.分式方程$\frac{x}{x-1}$-1=$\frac{3}{(x-1)(x+2)}$的解为( )
| A. | x=1 | B. | x=-1 | C. | 无解 | D. | x=-2 |
12.如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )
| A. | 13 | B. | 17 | C. | 13或17 | D. | 以上都不是 |
 如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.