题目内容
9.(1)计算:(a-b)(a2+ab+b2)(2)利用所学知识以及(1)所得等式,化简代数式$\frac{{m}^{3}-{n}^{3}}{{m}^{2}+mn+{n}^{2}}$÷$\frac{{m}^{2}-{n}^{2}}{{m}^{2}+2mn+{n}^{2}}$.
分析 (1)根据多项式乘以多项式法则计算即可得;
(2)利用(1)种结果将原式分子、分母因式分解,再约分即可得.
解答 解:(1)原式=a3+a2b+ab2-a2b-ab2-b3=a3-b3;
(2)原式=$\frac{(m-n)({m}^{2}+mn+{n}^{2})}{{m}^{2}+mn+{n}^{2}}$•$\frac{(m+n)^{2}}{(m+n)(m-n)}$
=(m-n)•$\frac{m+n}{m-n}$
=m+n.
点评 本题主要考查多项式乘以多项式及分式的乘法,根据多项式乘法得出立方差公式是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
20.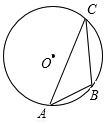 如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
 如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 2 |
4.在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=$\frac{1}{x}$相交于点A、B,且AC+BC=4,则△OAB的面积为( )
| A. | 2$\sqrt{3}$+3或2$\sqrt{3}$-3 | B. | $\sqrt{2}$+1或$\sqrt{2}$-1 | C. | 2$\sqrt{3}$-3 | D. | $\sqrt{2}$-1 |
 如图,直线MN交⊙O于A、B两点,AC是⊙O的直径,AD平分∠CAM交⊙O于D,过点D作⊙O的切线交MN于点E.
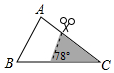
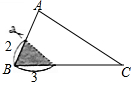
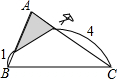
如图,直线MN交⊙O于A、B两点,AC是⊙O的直径,AD平分∠CAM交⊙O于D,过点D作⊙O的切线交MN于点E.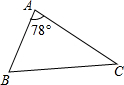 如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )