题目内容
15.关于x的方程mx2-4x-m+5=0,有以下说法:①当m=0时,方程只有一个实数根;②当m=1时,方程有两个相等的实数根;③当m=-1时,方程没有实数根.则其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 ①将m=0代入原方程,解之即可得出x的值,由此可得出说法①成立;②将m=1代入原方程,由根的判别式△=0,可得出说法②正确;③将m=-1代入原方程,由根的判别式△=40>0,可得出说法③不正确.综上即可得出结论.
解答 解:①当m=0时,原方程为-4x+5=0,
解得:x=$\frac{5}{4}$,
∴当m=0时,方程只有一个实数根;
②当m=1时,原方程为x2-4x+4=0,
∵△=(-4)2-4×1×4=0,
∴当m=1时,方程有两个相等的实数根;
③当m=-1时,原方程为x2+4x-6=0,
∵△=42-4×1×(-6)=40>0,
∴当m=-1时,方程有两个不相等的实数根.
综上所述:正确的说法有①②.
故选A.
点评 本题考查了根的判别式以及解一元一次方程,将m的值代入原方程结合根的判别式逐一分析三个说法的正误是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.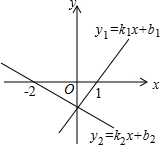 若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )
若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )
 若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )
若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )| A. | y1>y2 | B. | k1>k2 | C. | b1>b2 | D. | x=-2时y1=0 |
20.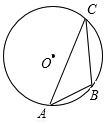 如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
 如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 2 |
7.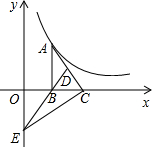 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
4.在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=$\frac{1}{x}$相交于点A、B,且AC+BC=4,则△OAB的面积为( )
| A. | 2$\sqrt{3}$+3或2$\sqrt{3}$-3 | B. | $\sqrt{2}$+1或$\sqrt{2}$-1 | C. | 2$\sqrt{3}$-3 | D. | $\sqrt{2}$-1 |
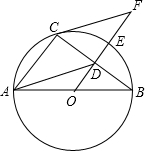 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
 如图所示,两个直角三角形的直角顶点重合,如果∠AOD=128°,那么∠BOC=52°.
如图所示,两个直角三角形的直角顶点重合,如果∠AOD=128°,那么∠BOC=52°.