题目内容
16.化简:$\frac{x+3}{{x}^{2}-2x+1}$÷$\frac{{x}^{2}+3x}{(x-1)^{2}}$=$\frac{1}{x}$.分析 根据分式的乘除法的法则进行计算即可.
解答 解:$\frac{x+3}{{x}^{2}-2x+1}$÷$\frac{{x}^{2}+3x}{(x-1)^{2}}$=$\frac{x+3}{(x-1)^{2}}$•$\frac{(x-1)^{2}}{x(x+3)}$=$\frac{1}{x}$,
故答案为:$\frac{1}{x}$.
点评 此题考查了分式的化简,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.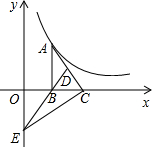 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
4.在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=$\frac{1}{x}$相交于点A、B,且AC+BC=4,则△OAB的面积为( )
| A. | 2$\sqrt{3}$+3或2$\sqrt{3}$-3 | B. | $\sqrt{2}$+1或$\sqrt{2}$-1 | C. | 2$\sqrt{3}$-3 | D. | $\sqrt{2}$-1 |
8.将函数y=x2的图象用下列方法平移后,所得的图象不经过点A(1,4)的方法是( )
| A. | 向左平移1个单位 | B. | 向右平移3个单位 | C. | 向上平移3个单位 | D. | 向下平移1个单位 |
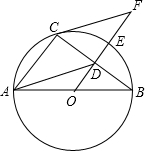 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC. 如图,在?ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}$BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
如图,在?ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}$BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
 如图所示,两个直角三角形的直角顶点重合,如果∠AOD=128°,那么∠BOC=52°.
如图所示,两个直角三角形的直角顶点重合,如果∠AOD=128°,那么∠BOC=52°.