题目内容
12. 如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.
如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.
分析 (1)连结OD,如图,由EF=ED得到∠EFD=∠EDF,再利用对顶角相等得∠EFD=∠CFO,则∠CFO=∠EDF,由于∠OCF+∠CFO=90°,∠OCF=∠ODF,则∠ODC+∠EDF=90°,于是根据切线的判定定理可得DE是⊙O的切线;
(2)由OF:OB=1:3得到OF=1,BF=2,设BE=x,则DE=EF=x+2,根据圆周角定理,由AB为直径得到∠ADB=90°,接着证明△EBD∽△EDA,根据相似三角形的性质即可得到结论.
解答 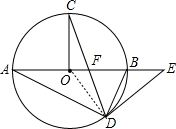 (1)证明:连结OD,如图,
(1)证明:连结OD,如图,
∵EF=ED,
∴∠EFD=∠EDF,
∵∠EFD=∠CFO,
∴∠CFO=∠EDF,
∵OC⊥OF,
∴∠OCF+∠CFO=90°,
而OC=OD,
∴∠OCF=∠ODF,
∴∠ODC+∠EDF=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵OF:OB=1:3,
∴OF=1,BF=2,
设BE=x,则DE=EF=x+2,
∵AB为直径,
∴∠ADB=90°,
∴∠ADO=∠BDE,
而∠ADO=∠A,
∴∠BDE=∠A,
而∠BED=∠DAE,
∴△EBD∽△EDA,
∴$\frac{DE}{AE}$=$\frac{BE}{DE}$,即$\frac{x+2}{6+2}$=$\frac{x}{x+2}$,
∴x=2,
∴BE=2.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.若a=-22,b=(-2)-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则a,b,c,d的大小关系是( )
| A. | b<d<c<a | B. | a<b<d<c | C. | b<a<d<c | D. | a<d<b<c |
3.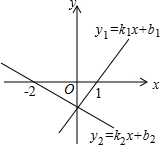 若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )
若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )
 若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )
若两个一次函数y1=k1x+b1和y2=k2x+b2的图象如图所示,则下列说法正确的是( )| A. | y1>y2 | B. | k1>k2 | C. | b1>b2 | D. | x=-2时y1=0 |
20.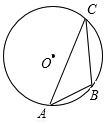 如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
 如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )
如图,A,B,C三点都在⊙O上,∠ACB=30°,AB=2$\sqrt{3}$,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 2 |
7.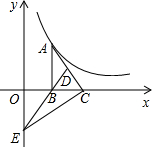 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
4.在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=$\frac{1}{x}$相交于点A、B,且AC+BC=4,则△OAB的面积为( )
| A. | 2$\sqrt{3}$+3或2$\sqrt{3}$-3 | B. | $\sqrt{2}$+1或$\sqrt{2}$-1 | C. | 2$\sqrt{3}$-3 | D. | $\sqrt{2}$-1 |

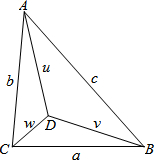 已知,如图,△ABC的三条边BC=a,CA=b,AB=c,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=u,DB=v,DC=w.
已知,如图,△ABC的三条边BC=a,CA=b,AB=c,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=u,DB=v,DC=w.