题目内容
5.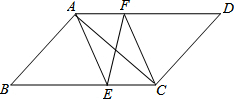 如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,求证:
如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,求证:(1)AE∥CF;
(2)BE=DF.
分析 (1)先由平行四边形的性质可得:AD∥BC、∠BAD=∠BCD,进而可得AF∥CE,然后由AE,CF分别平分∠BAD和∠BCD,可得∠BAE=∠DAE=$\frac{1}{2}$∠BAD,∠BCF=∠DCF=$\frac{1}{2}$∠BCD,从而可得∠DAE=∠BCF,然后由AD∥BC,根据两直线平行,内错角相等,可得∠DAE=∠BEA,从而可得∠BEA=∠BCF,然后由同位角相等,两直线平行即可判断AE∥CF;
(2)根据两组对边分别平行的四边形是平行四边形,即可证明四边形AECF是平行四边形,再利用平行四边形的性质解答即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC、∠BAD=∠BCD,
∴∠DAE=∠BEA,AF∥EC,
∵AE,CF分别平分∠BAD和∠BCD,
∴∠BAE=∠DAE=$\frac{1}{2}$∠BAD,∠BCF=∠DCF=$\frac{1}{2}$∠BCD,
∴∠DAE=∠BCF,
∴∠BEA=∠BCF,
∴AE∥CF;
(2)∵AE∥CF,AD∥BC,
∴四边形AECF是平行四边形,
∴AF=CE,
∵AD=BC,
∴BE=DF.
点评 本题考查了平行四边形的性质以及判定方法,证明∠AEB=∠FCB,得到AE∥CF是证明的关键.

练习册系列答案
相关题目
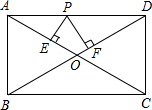 如图,在矩形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F.如果AB=5,AD=9.那么PE+PF的值.
如图,在矩形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F.如果AB=5,AD=9.那么PE+PF的值.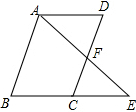 如图,C为BE的中点,四边形ABCD为平行四边形,AE与CD相交于点F.求证:AF=EF.
如图,C为BE的中点,四边形ABCD为平行四边形,AE与CD相交于点F.求证:AF=EF.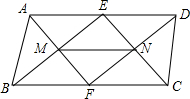 如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.
如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC. 平行四边形ABCD的两条对角线AC,BD相交于点O.
平行四边形ABCD的两条对角线AC,BD相交于点O. 在矩形ABCD中,点E是BC上一点,DF=DC,DF⊥AE,垂足为F.求证:AE=AD.
在矩形ABCD中,点E是BC上一点,DF=DC,DF⊥AE,垂足为F.求证:AE=AD.