题目内容
16.在菱形ABCD中,周长为52,BD=10,则AC的长为24,菱形的面积为120.分析 菱形对角线互相垂直平分,故△ABE为直角三角形,根据菱形周长可以计算AB的值,在Rt△ABE中,已知AB,BE根据勾股定理可以计算AE的长,根据AE即可计算CD的长,根据菱形的对角线的长度即可计算菱形ABCD的面积.
解答 解:(1)菱形对角线互相垂直平分,
故△ABE为直角三角形,
菱形ABCD的周长为52,
则AB=13,
∵BD=10,
∴BE=5cm,
在Rt△ABE中,AB=13,BE=5,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=12,
∴AC=2AE=24;
(2)菱形的对角线长为BD=10,AC=24,
∴菱形ABCD的面积S=$\frac{1}{2}$BD•AC=$\frac{1}{2}$×10×24=120,
故答案为:24,120.
点评 本题考查了勾股定理在直角三角形中的运用,考查了菱形对角线互相平分的性质,本题中正确计算BE的长是解题的关键.

练习册系列答案
相关题目
8.若一个三角形三边长均为奇数,则此三角形( )
| A. | 一定是直角三角形 | B. | 一定是等腰三角形 | ||
| C. | 一定不是直角三角形 | D. | 一定不是等腰三角形 |
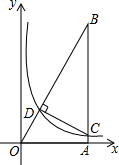 如图,Rt△AOB中,点A,B的坐标分别为(4,0),(4,8),C为AB上一点,双曲线y=$\frac{k}{x}$(k>0)经过点C,交OB于点D,且CD⊥OB.
如图,Rt△AOB中,点A,B的坐标分别为(4,0),(4,8),C为AB上一点,双曲线y=$\frac{k}{x}$(k>0)经过点C,交OB于点D,且CD⊥OB. 如图.E是?ABCD内任一点,若S?ABCD=6,则S△ABE+S△CDE=3.
如图.E是?ABCD内任一点,若S?ABCD=6,则S△ABE+S△CDE=3.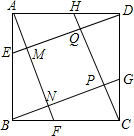 已知,如图,E,F,G,H分别是正方形ABCD各边的中点,AF,BC,CH,DE分别相交于点M,N,P,Q.求证:四边形MNPQ是正方形.
已知,如图,E,F,G,H分别是正方形ABCD各边的中点,AF,BC,CH,DE分别相交于点M,N,P,Q.求证:四边形MNPQ是正方形.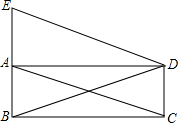 如图,矩形ABCD中,AC,BD是对角线,过顶点D作AC的平行线与BA的延长线相交于点E.
如图,矩形ABCD中,AC,BD是对角线,过顶点D作AC的平行线与BA的延长线相交于点E.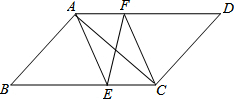 如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,求证:
如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,求证: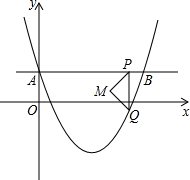 如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.