题目内容
17.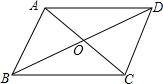 平行四边形ABCD的两条对角线AC,BD相交于点O.
平行四边形ABCD的两条对角线AC,BD相交于点O.(1)图中有哪些全等的三角形?有哪些相等的线段?
(2)若平行四边形ABCD的周长是20cm,△AOD的周长比△ABO的周长大6cm,求AB、AD的长.
分析 (1)根据平行四边形的性质:平行四边形对边相等,对角线互相平分可得AB=CD,AD=BC,AO=CO,BO=DO;然后可得四对全等三角形;
(2)根据题意可得AD+AB=10cm,根据△AOD的周长比△ABO的周长大6cm可得AD-AB=2cm,联立再解方程组可得答案.
解答 解:(1)全等三角形△AOB≌△COD,△AOD≌△COB,△ABD≌△CDB,△ACD≌△CAD,
相等的线段:AB=CD,AD=BC,AO=CO,BO=DO;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形ABCD的周长是20cm,
∴AD+AB=10cm,
∵△AOD的周长比△ABO的周长大6cm,
∴AD-AB=6cm,
∴$\left\{\begin{array}{l}{AD+AB=10}\\{AD-AB=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{AD=8}\\{AB=2}\end{array}\right.$,
∴AD=8cm,AB=2cm.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的对边相等;平行四边形的对角线互相平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若一个三角形三边长均为奇数,则此三角形( )
| A. | 一定是直角三角形 | B. | 一定是等腰三角形 | ||
| C. | 一定不是直角三角形 | D. | 一定不是等腰三角形 |
9.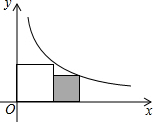 如图摆放的两个正方形,各有一个顶点在反比例函数y=$\frac{4}{x}$的图象上,则图中小正方形(阴影部分)的边长等于( )
如图摆放的两个正方形,各有一个顶点在反比例函数y=$\frac{4}{x}$的图象上,则图中小正方形(阴影部分)的边长等于( )
 如图摆放的两个正方形,各有一个顶点在反比例函数y=$\frac{4}{x}$的图象上,则图中小正方形(阴影部分)的边长等于( )
如图摆放的两个正方形,各有一个顶点在反比例函数y=$\frac{4}{x}$的图象上,则图中小正方形(阴影部分)的边长等于( )| A. | $\sqrt{5}$-1 | B. | $\sqrt{5}$-2 | C. | 1+$\sqrt{5}$ | D. | 4-$\sqrt{5}$ |
 如图.E是?ABCD内任一点,若S?ABCD=6,则S△ABE+S△CDE=3.
如图.E是?ABCD内任一点,若S?ABCD=6,则S△ABE+S△CDE=3.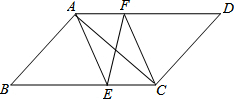 如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,求证:
如图所示,在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,求证: 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AD=3cm,求AB,AC的长.
如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AD=3cm,求AB,AC的长. 如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?
如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?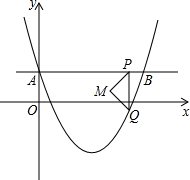 如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.