题目内容
10．
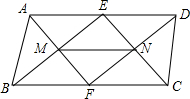如图所示，已知在?ABCD中，E，F分别是AD，BC的中点，求证：MN∥BC．
分析 首先根据线段中点的定义以及平行四边形的性质得出AD∥BC，AE=BF，DE=CF，那么四边形AEFB，CDEF都是平行四边形，由平行四边形对角线互相平分得出EM=MB，EN=NC，即M、N分别是EB、EC的中点；然后根据三角形的中位线定理，可得MN∥BC．
解答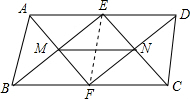 
证明：连结EF．
∵E、F分别是AD、BC的中点，
∴AE=DE，BF=CF，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴AE=BF，DE=CF，
∴四边形AEFB，CDEF都是平行四边形，
∴EM=MB，EN=NC，
∴MN是△ABC的中位线，
∴MN∥BC．
点评 （1）此题主要考查了三角形中位线定理的应用，要熟练掌握，解答此题的关键是要明确：三角形的中位线平行于第三边，并且等于第三边的一半．
（2）此题主要考查了平行四边形的判定与性质的应用，要熟练掌握，解答此题的关键是要明确：平行四边形的判定：一组对边平行且相等的四边形是平行四边形；平行四边形的性质：平行四边形的对边平行且相等；平行四边形的对角相等；平行四边形的对角线互相平分．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
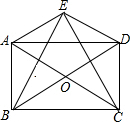如图，点E为?ABCD外一点，AE⊥EC，BE⊥ED，对角线AC、BD相交于点O．
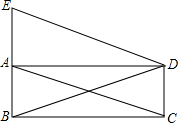如图，矩形ABCD中，AC，BD是对角线，过顶点D作AC的平行线与BA的延长线相交于点E．
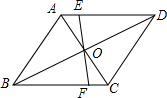如图，点O是菱形ABCD对角线的交点，过O点的直线AD、BC于点E、F．求证：AE+BF=AB．
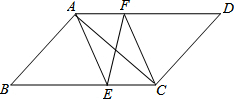如图所示，在平行四边形ABCD中，AE，CF分别平分∠BAD和∠BCD，求证：
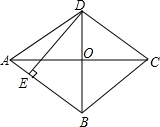如图，菱形ABCD中，对角线AC、BD相交于点O，DE⊥AB于点E，若菱形的周长为8$\sqrt{13}$，tan∠OAD=$\frac{2}{3}$，求DE的长．
如图所示，在?ABCD中，M，N是对角线BD上的两点，BN=DM，请判断AM与CN有怎样的数量关系，并说明理由，它们的位置关系如何呢？