��Ŀ����
8��ӣ����ֲ����ֲӣ�ҵijɱ���40��Ԫ/ǧ�ˣ��������г����У�ӣ����δ��45���ڵ���������n��ǧ�ˣ���ʱ���x���죩�Ĺ�ϵ��ͼ��ʾ��| ʱ�䣨�죩 | 1 | 2 | 6 | 20 | 35 | 41 | �� |
| ��������n��ǧ�ˣ� | 210 | 220 | 260 | 400 | 550 | 610 | �� |
��1��������һ�κ��������κ����ͷ�����������֪ʶ��ֱ��д��n��x�Ĺ�ϵʽ��
��2����Ԥ��δ��45������һ�������������������������Ƕ��٣�
��3����ʵ�����۵�ǰ15���У�ӣ����ֲ��ÿ����1ǧ��ӣ�������������벹��a��a��15��Ԫ��ͨ�����ۼ�¼���֣�ǰ15���У�ÿ��۳���������������ʱ����������������a��ȡֵ��Χ��
���� ��1����һ�κ���Ϊn=kx+b������ϵ�������ɵã�
��2�����ݣ�������������=ÿǧ�������������������1��x��30��31��x��45����������ֱ��г���������ʽ���䷽���϶��κ��������������ֵ�ȽϿɵã�
��3����ʵ��������ǰ15�����������ΪG�����ݣ�������������=ÿǧ������������������г�������ϵʽ����ǰ15����ÿ��۳���������������ʱ��������������ɵ������߶Գ��᷶Χ�������ɵ�a��ȡֵ��Χ��
��� �⣺��1���ӱ���ɿ���ÿ���ǰһ�������10���������ж�Ϊһ�κ�����ϵʽ��
��һ�κ���Ϊn=kx+b��
����1��210���ͣ�2��220������һ�κ���n=kx+b�У�
�ã�$\left\{\begin{array}{l}{k+b=210}\\{2k+b=220}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=10}\\{b=200}\end{array}\right.$��
��n=10x+200��
��2��������������ΪW��
��1��x��30ʱ��
W=��132-2x-40����10x+200��
=-20x2+520x+18400
=-20��x-13��2+21780��
��x=13ʱ��Wȡ�����ֵ21780Ԫ��
��31��x��45ʱ��
W=��82-$\frac{1}{3}$x-40����10x+200��
=-$\frac{10}{3}$x2+$\frac{1060}{3}$x+8400
=-$\frac{10}{3}$��x-53��2+$\frac{53290}{3}$��
�ߵ�x��53ʱ��W��x�����������
�൱x=45ʱ��Wȡ�����ֵ17550Ԫ��
��21780��17550��
�൱x=13ʱ��Wȡ�����ֵ21780Ԫ��
��Ԥ��δ��45���е�13��������������������������21780Ԫ��
��3����ʵ��������ǰ15�����������ΪG
G=��132-2x+a-40����200+10x��=-20x2+��520+10a��x+18400+200a
�������֪���ú����ĶԳ���x=-$\frac{520+10a}{2����-20��}$=13+$\frac{1}{4}$a��15��
��ã�a��8��
�֡�a��15��
��a��ȡֵ��ΧΪ��8��a��15��
���� ������Ҫ������κ�����ʵ��Ӧ��������������ȹ�ϵ�г�������ϵʽ�ǽ����ǰ������������۵��۵IJ�ͬ������������ǹؼ���

| A�� | ��-a��3+��-a��5 | B�� | ��-a��3•��-a��5 | C�� | ��-a3��5 | D�� | ��-a��10�£�-a2�� |
| A�� | 3x+3y=3xy | B�� | ��2x3��2=4x5 | C�� | -3x+2x=-x | D�� | y2•2y3=2y6 |
 ��ͼ����ABC�����������ΪA��1��4����B��5��1����C��1��9������˫����y=$\frac{k}{x}$��x��0���ڵ�һ���������ABC�н��㣬��k��ȡֵ��Χ��
��ͼ����ABC�����������ΪA��1��4����B��5��1����C��1��9������˫����y=$\frac{k}{x}$��x��0���ڵ�һ���������ABC�н��㣬��k��ȡֵ��Χ��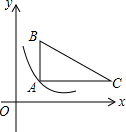 ��ͼ����ֱ������ϵ�У�Rt��ABCλ�ڵ�һ���ޣ�����ֱ�DZ�AC��AB�ֱ�ƽ����x�ᡢy�ᣬ��A������Ϊ��1��1����AB=2��AC=3��
��ͼ����ֱ������ϵ�У�Rt��ABCλ�ڵ�һ���ޣ�����ֱ�DZ�AC��AB�ֱ�ƽ����x�ᡢy�ᣬ��A������Ϊ��1��1����AB=2��AC=3��