如果在组成反比例函数$y=\frac{1-k}{x}$图象的每条曲线上.y都随x的增大而增大.那么k的取值范围是k＞1．题目和参考答案——青夏教育精英家教网—

题目内容

18．如果在组成反比例函数$y=\frac{1-k}{x}$图象的每条曲线上，y都随x的增大而增大，那么k的取值范围是k＞1．

分析根据反比例函数的增减性列出关于k的不等式，求出k的取值范围即可．

解答解：∵反比例函数$y=\frac{1-k}{x}$图象的每条曲线上，y都随x的增大而增大，
∴1-k＜0，解得k＞1．
故答案为：k＞1．

点评本题考查的是反比例函数的性质，熟知反比例函数y=$\frac{k}{x}$（k≠0）的图象是双曲线，当k＜0时，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大是解答此题的关键．

练习册系列答案

时间（天）	1	2	6	20	35	41	…
日销售量n（千克）	210	220	260	400	550	610	…

前30天的价格y₁（元/千克）与时间x（天）的关系式为y₁=132-2x（1≤x≤30且x为整数）；后20天的价格y₂与时间x（天）的关系式为y₂=82-$\frac{1}{3}$x（31≤x≤45且x为整数）．
（1）请利用一次函数、二次函数和反比例函数的知识，直接写出n与x的关系式；
（2）请预测未来45天中那一天的利润最大？最大的日销售利润是多少？
（3）在实际销售的前15天中，樱桃种植户每销售1千克樱桃政府决定给与补贴a（a≤15）元，通过销售记录发现，前15天中，每天扣除捐献后销售利润随时间天的增大而增大，求a的取值范围．

a²+a²=a⁴

（a²）³=a⁶

13．己知点M（m，4）在函数y=$-\frac{12}{x}$的图象上，则m=-3．

a+a²=a³

a⁶b÷a²=a³b

（-ab³）²=a²b⁶

7．在平面直角坐标系xOy中，图形W在坐标轴上的投影长度定义如下：设点P（x₁，y₁），Q（x₂，y₂）是图形W上的任意两点．若|x₁-x₂|的最大值为m，则图形W在x轴上的投影长度l₁=M；若|y₁-y₂|的最大值为n，则图形W在y轴上的投影长度l_y=n．如图1，图形W在x轴上的投影长度l_x=|3-1|=2；在y轴上的投影长度l_y=|4-0|=4．
（1）已知点A（3，3），B（4，1）．如图2所示，若图形W为△OAB，则l_x4，l_y3．
（2）已知点C（4，0），点D在直线y=2x+6上，若图形W为△OCD．当l_x=l_y时，求点D的坐标．
（3）若图形W为函数y=x²（a≤x≤b）的图象，其中0≤a＜b．当该图形满足l_x=l_y≤1时，请直接写出a的取值范围．

8．

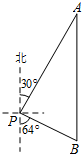如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处．海轮沿正南方向航行一段时间后，到达位于灯塔P的南偏东64°方向上的B处．求海轮所在的B处与灯塔P的距离．（结果精确到0.1海里）（参考数据：sin64°=0.90，cos64°=0.44，tan64°=2.05）

试题分类