题目内容
20.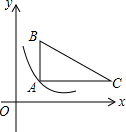 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.(1)求BC边所在直线的解析式;
(2)若反比例函数y=$\frac{m}{x}(x>0)$的图象经过点A,求m的值;
(3)若反比例函数y=$\frac{n}{x}(x>0)$的图象与△ABC有公共点,请直接写出n的取值范围.
分析 (1)根据题意得出B、C两点的坐标,利用待定系数法求出直线BC的解析式即可;
(2)把A点坐标代入反比例函数y=$\frac{m}{x}$(x>0),求出m的值即可;
(3)根据反比例函数y=$\frac{n}{x}(x>0)$的图象与△ABC有公共点可知,当反比例函数经过点A时有最小值,反比例函数与线段BC相切时时有最大值可得出n的取值范围.
解答 解:(1)∵Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3,
∴B(1,3),C(4,1),
设直线BC的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}k+b=3\\ 4k+b=1\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{2}{3}\\ b=\frac{11}{3}\end{array}\right.$,
∴BC边所在直线的解析式为:y=-$\frac{2}{3}$x+$\frac{11}{3}$;
(2)∵反比例函数y=$\frac{m}{x}(x>0)$的图象经过点A(1,1),
∴m=1;
(3)∵反比例函数y=$\frac{n}{x}$的图象与△ABC有公共点,
∴当函数经过A(1,1)时,n=1;
当函数图象经过点C(4,1)时,n=4,
当反比例函数与线段BC相切时,设y=$\frac{n}{x}$过BC上一点(a,-$\frac{2}{3}$a+$\frac{11}{3}$),
则n=a(-$\frac{2}{3}$a+$\frac{11}{3}$)=-$\frac{2}{3}$(a-$\frac{11}{4}$)2+$\frac{121}{24}$,
∴n最大=$\frac{121}{24}$.
∴1≤n≤$\frac{121}{24}$.
点评 本题考查的是反比例函数的性质,熟知反比例函数图象上点的坐标一定适合此函数的解析式是解答此题的关键.


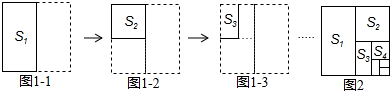
根据排列规律,从2015到2017的箭头依次为( )
| A. | ↓→ | B. | →↓ | C. | ↑→ | D. | →↑ |
| A. | a | B. | -a | C. | 2b+a | D. | 2b-a |
| 时间(天) | 1 | 2 | 6 | 20 | 35 | 41 | … |
| 日销售量n(千克) | 210 | 220 | 260 | 400 | 550 | 610 | … |
(1)请利用一次函数、二次函数和反比例函数的知识,直接写出n与x的关系式;
(2)请预测未来45天中那一天的利润最大?最大的日销售利润是多少?
(3)在实际销售的前15天中,樱桃种植户每销售1千克樱桃政府决定给与补贴a(a≤15)元,通过销售记录发现,前15天中,每天扣除捐献后销售利润随时间天的增大而增大,求a的取值范围.
| A. | x•x2=x2 | B. | (a3)2=a5 | C. | a+2a=3a | D. | (ab)2=ab2 |
| A. | a2+a2=a4 | B. | 2a2×a3=2 | C. | (a2)3=a6 | D. | 3a-2a=1 |
| A. | -1+2 | B. | |-1| | C. | $\sqrt{(-2)^{2}}$ | D. | -2-1 |