题目内容
18. 如图,△ABC的三个顶点别为A(1,4),B(5,1),C(1,9),若双曲线y=$\frac{k}{x}$(x>0)在第一象限内与△ABC有交点,求k的取值范围.
如图,△ABC的三个顶点别为A(1,4),B(5,1),C(1,9),若双曲线y=$\frac{k}{x}$(x>0)在第一象限内与△ABC有交点,求k的取值范围.
分析 利用待定系数法把三点分别代入求出k的值即可解决问题.
解答 解:当y=$\frac{k}{x}$经过点A(1,4)时,得k=4,
当y=$\frac{k}{x}$经过点B(5,1)时,得k=5,
当y=$\frac{k}{x}$经过点C(1,9)时,得k=9,
∵直线BC的解析式为y=-2x+11.
由$\left\{\begin{array}{l}{y=-2x+11}\\{y=\frac{k}{x}}\end{array}\right.$消去y得到,2x2-11x+k=0,
当△=0时,k=$\frac{121}{8}$,
综上所述k的范围为:4≤k≤$\frac{121}{8}$.
点评 本题考查反比例函数的性质、解题的关键是掌握待定系数法确定函数解析式,需要理解题意,属于中考常考题型.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
6.反比例函数y=(2m-1)${x}^{{m}^{2}-1}$,当x>0时,y随x的增大而增大,则m的值是( )
| A. | ±1 | B. | 小于$\frac{1}{2}$的实数 | C. | -1 | D. | 1 |
10.将正整数1,2,3,4…按以下方式排列

根据排列规律,从2015到2017的箭头依次为( )

根据排列规律,从2015到2017的箭头依次为( )
| A. | ↓→ | B. | →↓ | C. | ↑→ | D. | →↑ |
7.下列计算正确的是( )
| A. | a3÷a=a3 | B. | a+a=2a | C. | (a3)2=a9 | D. | a2•a2=2a2 |
8.樱桃种植户种植樱桃的成本是40(元/千克),经过市场调研,樱桃在未来45天内的日销售量n(千克)与时间的x(天)的关系如图所示:
前30天的价格y1(元/千克)与时间x(天)的关系式为y1=132-2x(1≤x≤30且x为整数);后20天的价格y2与时间x(天)的关系式为y2=82-$\frac{1}{3}$x(31≤x≤45且x为整数).
(1)请利用一次函数、二次函数和反比例函数的知识,直接写出n与x的关系式;
(2)请预测未来45天中那一天的利润最大?最大的日销售利润是多少?
(3)在实际销售的前15天中,樱桃种植户每销售1千克樱桃政府决定给与补贴a(a≤15)元,通过销售记录发现,前15天中,每天扣除捐献后销售利润随时间天的增大而增大,求a的取值范围.
| 时间(天) | 1 | 2 | 6 | 20 | 35 | 41 | … |
| 日销售量n(千克) | 210 | 220 | 260 | 400 | 550 | 610 | … |
(1)请利用一次函数、二次函数和反比例函数的知识,直接写出n与x的关系式;
(2)请预测未来45天中那一天的利润最大?最大的日销售利润是多少?
(3)在实际销售的前15天中,樱桃种植户每销售1千克樱桃政府决定给与补贴a(a≤15)元,通过销售记录发现,前15天中,每天扣除捐献后销售利润随时间天的增大而增大,求a的取值范围.
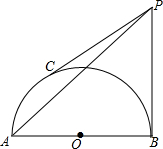 如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.
如图,AB为半圆O的直径,C为半圆弧上的三等分点,半圆O的切线PB和PC相交于点P,若AB=4cm,求PA的长.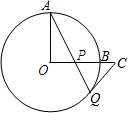 如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.
如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.