题目内容
20.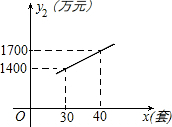 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.(1)直接写出y2(2)与x之间的函数关系式;
(3)求月产量x的取值范围;
(4)当月产量x(套)为多少时,这种产品的利润W(万元)最大?最大利润是多少?
分析 (1)根据题意可以设出y2与x之间的函数关系式,然后根据图象中的数据即可求得函数的解析式;
(2)根据题意可以列出相应的不等式组,从而可以求得x的取值范围;
(3)根据题意可以得到W与x函数关系式,然后化为顶点式,再根据x的取值范围,即可求得W的最大值.
解答 解:(1)设y2与x的函数关系式为y2=kx+b,
$\left\{\begin{array}{l}{1400=30k+b}\\{1700=40k+b}\end{array}\right.$,得$\left\{\begin{array}{l}{k=30}\\{b=500}\end{array}\right.$,
∴y2与x之间的函数关系式是y2=30x+500;
(2)由题意可得,
$\left\{\begin{array}{l}{190-2x≥120}\\{\frac{30x+500}{x}≤50}\end{array}\right.$,
解得,25≤x≤35,
即月产量x的取值范围是25≤x≤35;
(3)由题意可得,
W=x[190-2x-$\frac{30x+500}{x}$]=-2(x-40)2+2700,
∵25≤x≤35,
∴x=35时,W取得最大值,此时W=2650,
即当月产量x(套)为35套时,这种产品的利润W(万元)最大,最大利润是2650万元.
点评 本题考查二次函数的应用、一次函数的应用,一元一次不等式组的应用,解答此类题目的关键是明确题意,找出所求问题需要的条件,利用二次函数的顶点式求函数的最值,注意自变量的取值范围.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
18.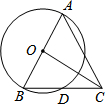 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )| A. | 4 | B. | $\frac{5}{2}$$\sqrt{3}$ | C. | $\frac{9}{5}$$\sqrt{5}$ | D. | $\frac{\sqrt{65}}{2}$ |
 如图,已知AB=CD,AB∥CD,BE=CF,求证:AF∥ED.
如图,已知AB=CD,AB∥CD,BE=CF,求证:AF∥ED.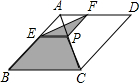 如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.
如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.

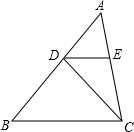 如图,在△ABC中,AB=4,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值为$\frac{1}{4}$.
如图,在△ABC中,AB=4,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值为$\frac{1}{4}$.